Selection Sort: Algorithm, Program in C

by

Selection Sort is a simple comparison-based sorting algorithm. It divides the input list into two parts: the sublist of items already sorted, which is built up from left to right at the front (left) of the list, and the sublist of items remaining to be sorted that occupy the rest of the list.

Initially, the sorted sublist is empty, and the unsorted sublist is the entire input list. The algorithm proceeds by finding the smallest (or largest, depending on sorting order) element in the unsorted sublist, exchanging (swapping) it with the leftmost unsorted element (putting it in sorted order), and moving the sublist boundaries one element to the right.

Selection sort is a sorting algorithm that has an O(n2) time complexity for all the cases like best, average, and worst case.

How selection Sort works

  • Suppose we have an array Arr of length n, where n is 0…..n and elements are arr[0], arr[1], arr[2]….arr[n]
  • In the Selection sort technique to sort an array arr, first find the minimum element of the array.
  • After finding the minimum in the array exchange it with the first element.
  • So in the first pass, we have a minimum element of an array at the first position.
  • Similarly in the second pass, the second minimum will be at the second position of the array.
  • The same procedure will be followed by the rest of the element of the array.
  • In each pass, one element will be sorted.
  • Selection sort performs worse than insertion sort because in best case time complexity of insertion sort is O(n) but for selection sort, best case time complexity is O(n^2).

How selection sort works with example

Here we will sort the below array using selection sort.

Selection Sort

After First Pass

In first pass at position 1 index 0, array element 1 is sorted.

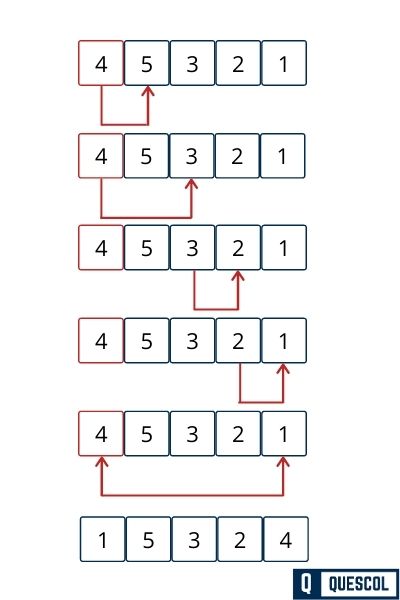
Selection Sort algorithm

After Second Pass

In Second pass at position 2 index 1, array element 2 is sorted.

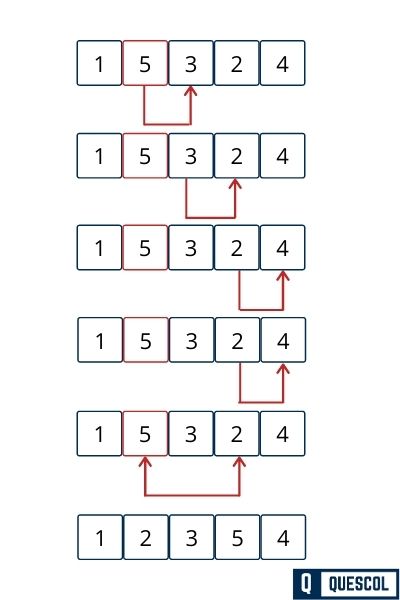
Selection Sort program

After Third Pass

In the third pass at position 3 index 2, array element 3 is sorted.

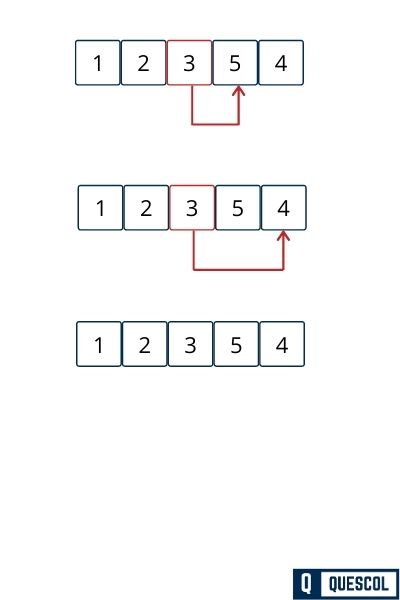
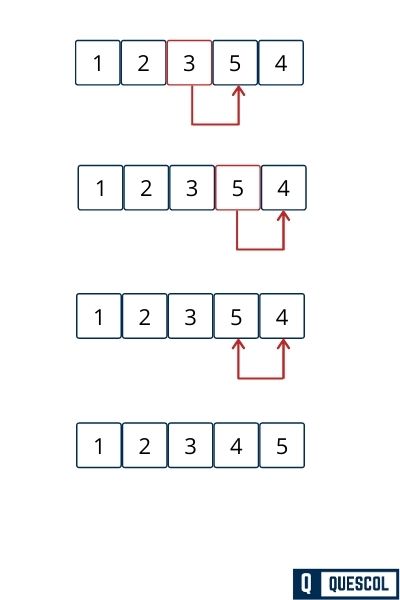
After Fourth Pass

In the Fourth pass at position 4 index 3, array element 4 is sorted. And as well as our array become sorted

Selection Sort Algorithm

Step 1 − Set the first element of array means 0 location element as MIN
Step 2 − Find the minimum element in the array
Step 3 − If minimum found then swap it with the value of location MIN
Step 4 − Increase MIN by 1 to point to the next element of the array
Step 5 − Repeat until the list is sorted

Psuedo Code of Selection Sort

SMALLEST (ARR, K, N, POS)
Step 1: [INITIALIZE] SET MIN = ARR[K]
Step 2: [INITIALIZE] SET POS=K
Step 3: Repeat for J= K+1 to N
         IF MIN > ARR[J]
          SET MIN = ARR[J]
          SET POS=J
        [END OF IF]
       [END OF LOOP]
Step 4: RETURN POS

C Program for Selection sort

#include <stdio.h>
#include<conio.h>
 
void selectionSort(int arr[], int size) {
  for (int step = 0; step < size - 1; step++) {
    int min = step;
    int temp;
    for (int i = step + 1; i < size; i++) {
      if (arr[i] < arr[min])
        min = i;
    }
    temp = arr[min];
    arr[min] = arr[step];
    arr[step] = temp;
  }
}
 
int main() {
  int arr[100],i,j,n,key;
  printf("Enter the number of elements you want to sort:\n");
  scanf("%d",&n);
  printf("Now enter the %d elements you want to sort: \n",n);
  for(i=0;i<n;i++){
    scanf("%d",&arr[i]);
  }
  printf("before sorting:\n");
  for(i=0;i<n;i++){
    printf("%d \t",arr[i]);
  }
  selectionSort(arr, n);
  printf("\n After Sorting using Selection Sort:\n");
  for (int i = 0; i < n; ++i) {
    printf("%d \t", arr[i]);
  }
  printf("\n");
  getch();
}

Output:

Enter the number of elements you want to sort:
6
Now enter the 6 elements you want to sort: 
23
11
12
54
2
11
before sorting:
23      11      12      54      2       11 
 After Sorting using Selection Sort:
2       11      11      12      23      54

Explanation of Selection sort program

This C program implements the Selection Sort algorithm to sort an array of integers in ascending order. Here’s a step-by-step explanation of how this program works:

Including Header Files

#include<stdio.h>
#include<conio.h>
  • stdio.h is included for input/output operations (printf, scanf).
  • conio.h is included for console input/output operations, like getch() which waits for a character input to pause the program’s termination, allowing users to see the output before the console window closes.

Selection Sort Function

void selectionSort(int arr[], int size) {

This function sorts the given array arr of size size using the selection sort algorithm.

  • It iterates through the array with step indicating the current position being filled with the correct value.
  • For each position, it finds the index of the smallest value (min) in the unsorted part of the array (from step + 1 to size - 1).
  • It then swaps the smallest found value with the value at the current position step.

The Main Function

int main() {

The main function is the entry point of the program.

  • It asks the user for the number of elements they want to sort (n) and reads them into an array arr.
  • It prints the array before sorting to show the original order.
  • It calls selectionSort(arr, n) to sort the array.
  • After sorting, it prints the sorted array.
  • Finally, getch() is called to wait for a keystroke before closing, allowing the user to see the sorted array.

How Selection Sort Works in This Program

  1. Iterate through each element of the array except the last one. Each iteration of step marks where the next smallest unsorted element will go.
  2. Find the smallest element in the rest of the array (i.e., from arr[step+1] to arr[size-1]).
  3. Swap the smallest element found with the element at the current step index.
  4. Repeat this process until the array is sorted.

Input/Output Process

  • The user is prompted to enter the number of elements (n) and then the elements themselves.
  • The program displays the array before and after applying the selection sort algorithm.

Time Complexity of Selection Sort

Best Case Complexity: O(n2)
In selection best-case scenario is when an array is already sorted in ascending order.

Average Case Complexity: O(n2)
In selection Average case scenario is when an array is in jumbled order means neither ascending nor descending.

Worst Case Complexity: O(n2)
In selection worst-case scenario is when an array is in descending order and we want to sort it in ascending order.

Space Complexity of Selection Sort

Space complexity is O(1) because an extra variable temp is used.

Advantages of Selection Sort

  • Selection Sort is easy to implement.
  • It can be used for small data sets.
  • It is more efficient than bubble sort because swaps are O(n) as compared to O(n2) of bubble sort