Insertion sort algorithm and program in C

Insertion Sort is one of the simplest sorting algorithms that compare each array element with new elements that we want to insert in an array. It will insert a new element when found the correct position because the array should maintain order.

Let’s understand it in brief

Suppose you have an array of 5 cards of a deck, and they are sorted in ascending order. Now you want to insert a new card and condition is all card should be in ascending order after insertion of the new card.

Now to insert a new card at the correct position, you have to start from the first card and then compare each card with a new card. Once you find the correct position, then you can insert the new card there. This procedure is followed by each element of the insertion sort to maintain the order of an array.

Above is the brief introduction of how insertion sort works.

Insertion Sort Algorithm

Step 1. If there is only one element or the first element in an array, it behaves as a sorted array.
Step 2. Now pick the new element which you want to insert.
Step 3. Compare the new picked element with the sorted element of an array.
Step 4. Insert the value if the correct position is found.
Step 5. Repeat step 2 to step 4 until all element is inserted in an array.

How Insertion sort works with an example

Here we will sort the below array using selection sort.

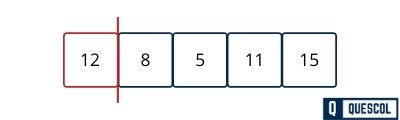
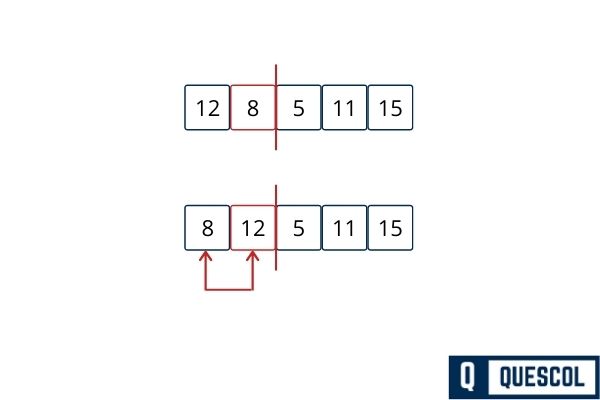
First Pass

Second Pass

Third Pass

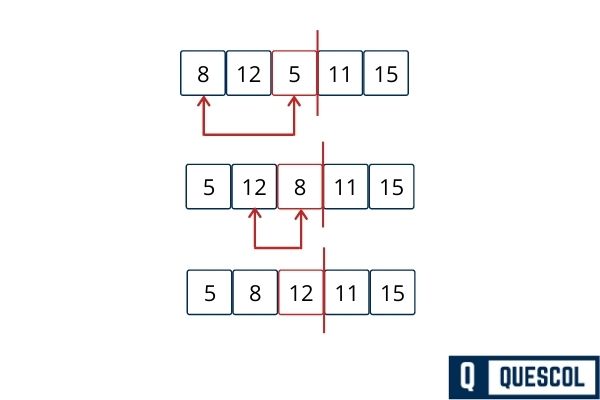
Fourth Pass

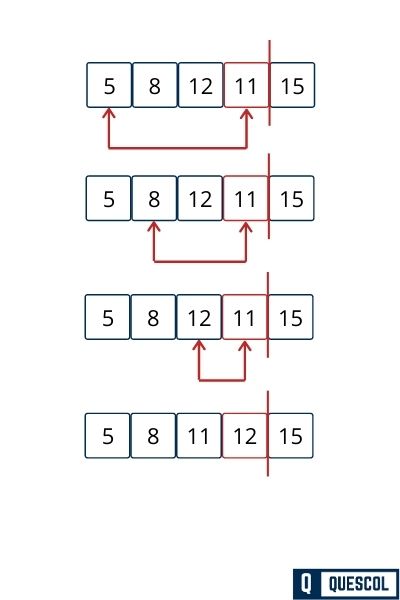
Fifth Pass

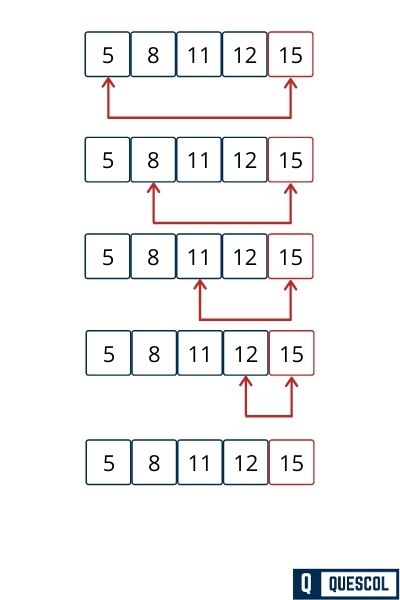
Pseudo-code of insertion sort

i ← 1
while i < length(A) x ← A[i] j ← i - 1 while j >= 0 and A[j] > x
A[j+1] ← A[j]
j ← j - 1
end while
A[j+1] ← x[3]
i ← i + 1
end while

Complexity of Insertion Sort

Best-case performance O(n) comparisons, O(1) swaps
Average performance О(n2) comparisons and swaps
Worst-case performance О(n2) comparisons and swaps
Worst-case space complexity О(n) total, O(1) auxiliary

Insertion Sort Program in C

#include<stdio.h>
#include<conio.h>
void main(){
    int arr[100],i,j,n,key;
    printf("Enter the number of elements you want to sort:\n");
    scanf("%d",&n);
    printf("Now enter the %d elements you want to sort: \n",n);
    for(i=0;i<n;i++){
        scanf("%d",&arr[i]);
    }
    printf("before sorting:\n");
    for(i=0;i<n;i++){
        printf("%d \t",arr[i]);
    }
    for(i=1;i<n;i++){
        key=arr[i];
        j=i-1;
        while(j>=0 && arr[j]>key){
            arr[j+1]=arr[j];
            j=j-1;
        }
        arr[j+1]=key;
    }
    printf("\n");
    printf("after sorting:\n");
    for(i=0;i<n;i++){
        printf("%d\t",arr[i]);
    }
    getch();
}

Output:

Enter the number of elements you want to sort:
5
Now enter the 5 elements you want to sort: 
32
11
33
67
1
before sorting:
32      11      33      67      1 
after sorting:
1       11      32      33      67

Characteristics of Insertion Sort

• Insertion sort works perfectly for small data sets, but it takes time when the data set is large.
• It is inefficient for large data set.
• The space complexity of the Insertion sort is less because it takes a single additional memory space.
• Insertion sort is a stable sorting technique because it does not change the relative order of elements.

Complexity analysis of Insertion sort

Time Complexity

Best-case O(n):

It takes O(n) comparisons and O(1) swap to insert value in a sorted array in the best case. The best case means it can happen; the array elements are already sorted before applying Insertion sort. If we apply insertion sort on it, it will still take O(n) comparison in the best case.

Worst-case О(n2):
In the Worst case scenario, an array can be in descending order, but we want to sort array in ascending order. In the worst case, it takes n^2 comparison and swaps.

Average Case О(n2):
And On average, case elements have a random arrangement in an array. And it takes O(n^2) comparison and swap.

Space Complexity

Space Complexity: Θ(1)

Insertion sort takes O(1) additional memory space

---

[wpusb]