Bubble sort is a simple sorting method to sorts the array elements. In the bubble sorting technique each array element is compared to the adjacent elements of the array. If the lower index value is greater than the highest index position of the array then swap these two adjacent values to maintain ascending sorting order.
This process will continue till the element is available in an array.
In the first pass, the largest element of the array will be placed at its proper
position means at the end of the list.
A bubble sorting algorithm is not suitable for large data sets because average time complexity and worst-case time complexity are of Ο(n2) where n is the number of items.
How Bubble Sort Works
- Compare Adjacent Items: Starting from the beginning of the list, compare each pair of adjacent items.
- Swap if Necessary: If the first item in the pair is greater than the second, swap them. This step ensures that after each complete pass through the list, the largest unsorted item is moved to its correct position.
- Repeat: Continue making passes through the list, each time ignoring the last item (as it’s already in its correct place).
- End When Sorted: The algorithm stops when a pass through the list requires no swaps, meaning the list is sorted.
Sorting Using Bubble Sort
Suppose we have an array arr of size 5 with array element [12, 8, 5, 11, 15].
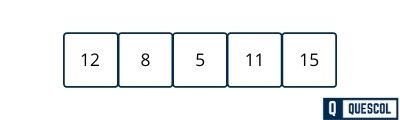
First Pass
- Compare 12 and 8. Since 12 > 8, swap them:
[8, 12, 5, 11, 15] - Compare 12 and 5. Since 12 > 5, swap them:
[8, 5, 12, 11, 15] - Compare 12 and 11. Since 12 > 11, swap them:
[8, 5, 11, 12, 15] - Compare 12 and 15. Since 12 < 15, do nothing:
[8, 5, 11, 12, 15]
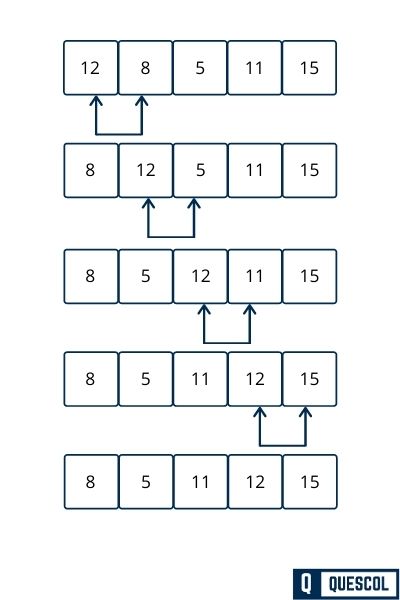
Second Pass
- Compare 8 and 5. Since 8 > 5, swap them:
[5, 8, 11, 12, 15] - Compare 8 and 11. Since 8 < 11, do nothing:
[5, 8, 11, 12, 15] - Compare 11 and 12. Since 11 < 12, do nothing:
[5, 8, 11, 12, 15] - No need to compare 12 and 15, as 15 is already in place.
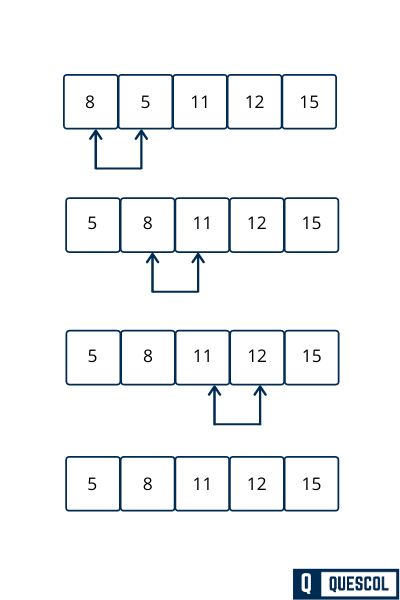
Third Pass
- Compare 5 and 8. Since 5 < 8, do nothing:
[5, 8, 11, 12, 15] - Compare 8 and 11. Since 8 < 11, do nothing:
[5, 8, 11, 12, 15] - There’s no need to compare further as the remaining elements are already sorted.
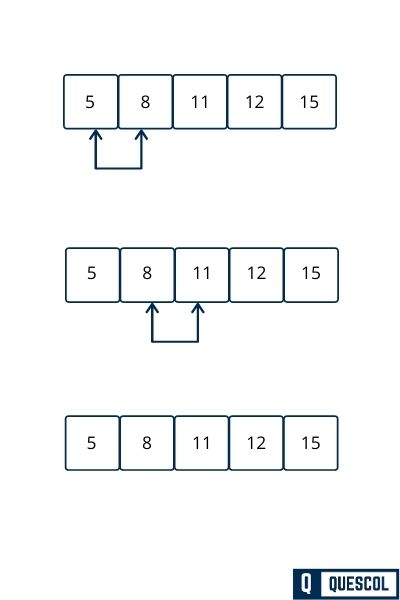
Fourth Pass
At this point, the array is sorted as [5, 8, 11, 12, 15]. Each step involved comparing adjacent elements and swapping them if they were in the wrong order. This process is repeated, ignoring the last element each time since it’s in its correct position, until no swaps are needed, indicating that the array is sorted.
Algorithm of Bubble Sort
begin BubbleSort(arr, n)
for I=0 to N-1
for J=0 to N-I
if arr[j] > arr[j+1]
swap(arr[j], arr[j+1])
end if
end for
end for
return arr
end BubbleSort
Bubble Sort Time Complexity
Best-case performance: O(n) comparisons, O(1) swaps
Average performance: О(n2) comparisons and swaps
Worst-case performance: О(n2) comparisons and swaps
Bubble Sort Program in C
#include<stdio.h>
#include<conio.h>
void main(){
int arr[100],i,j,n,key;
printf("Enter the number of elements you want to sort:\n");
scanf("%d",&n);
printf("Now enter the %d elements you want to sort: \n",n);
for(i=0;i<n;i++){
scanf("%d",&arr[i]);
}
printf("before sorting:\n");
for(i=0;i<n;i++){
printf("%d \t",arr[i]);
}
for(i=0;i<n;i++)
{
for(j=0;j<n-i-1;j++){
if(arr[j]>arr[j+1])
{
key=arr[j];
arr[j]=arr[j+1];
arr[j+1]=key;
}
}
}
printf("\n");
printf("after sorting:\n");
for(i=0;i<n;i++){
printf("%d \t",arr[i]);
}
getch();
}Output :
Enter the number of elements you want to sort:
5
Now enter the 5 elements you want to sort:
78
96
12
2
55
before sorting:
78 96 12 2 55
after sorting:
2 12 55 78 96 Advantages of Bubble Sort
- Simplicity: It’s straightforward to understand and implement, making it a good educational tool.
- Detects a Sorted List Early: If the list is already sorted (or nearly sorted), Bubble Sort can detect this and terminate early, making it efficient in such cases.
Real-Life Example of Bubble Sort
Imagine you have a deck of number cards spread out randomly. Using Bubble Sort, you start comparing each card to the next, swapping them to get them in order. You go through the deck several times, each time with one less card to compare, just like sorting your toy cars. By the end, your cards are neatly sorted from lowest to highest.
Conclusion
Bubble Sort, with its simplicity and intuitive process, is an excellent introduction to sorting algorithms, despite not being the most efficient for large datasets. It teaches important concepts in computer science, like iteration, comparisons, and swaps, which are foundational in more complex algorithms. Its straightforward logic mirrors everyday sorting processes, bridging abstract data structures with tangible, real-world tasks.
