Kruskal’s Algorithm follows the Greedy Algorithm to construct a Minimum Spanning Tree for a connected, weighted, and undirected graph. This algorithm treats the graph as a forest and its vertices as an individual tree. The aim of this algorithm is to find a subset of the edges that forms a tree that includes every vertex with minimum edges.
A single graph can have many different spanning trees. A minimum spanning tree for a weighted, connected, and the undirected graph is a spanning tree with the sum of edges weight is less than or equal to the sum of edges weight of every other spanning tree.
How Kruskal’s algorithm works
Kruskal’s algorithm follows a greedy algorithm to find a minimum spanning tree. In a greedy algorithm, it always choosing the next piece that offers the most local optimal solution of the problems where choosing locally optimal also leads to the global solution.
We start from adding edge with least weight and keep adding next edges that has least weight. Also, vertices should cover and minimum spanning tree properties should intact.
The steps for implementing Kruskal’s algorithm are as follows
Step 1: Remove all loops and parallel edges.
Step 2: Sort all the edges in non-decreasing order of their weight.
Step 3: Pick the least weightage edge and include this edge if it does not form a cycle. Else, discard it.
Step 4: Repeat step 2 until we get a minimum spanning tree.
Let’s See an Example to understand Kruskal’s algorithm
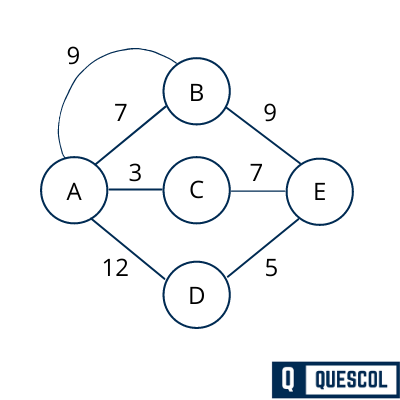
Step 1 – Remove all loops and Parallel Edges
After removing parallel edge from the graph, graph will look like below.
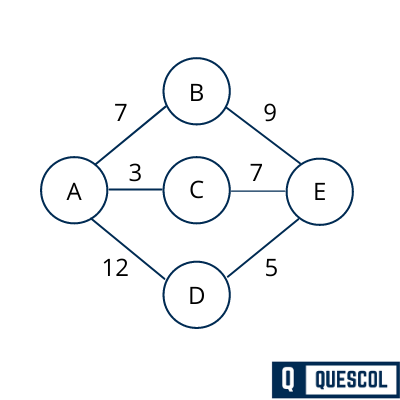
Step 2 – Sort all the edges in non-decreasing order of their weight
AC – 3, DE – 5, AB – 7, BE – 9, CE – 7, AD – 12
Step 3 – Pick the least weightage edge and include this edge
We will add edges to the graph beginning from the one which has the least weight. As well as also we will keep checking this edge should not form any cycle. In cycle will create by adding one edge or any other property that violates the spanning-tree property then we will not include the edge in the graph.
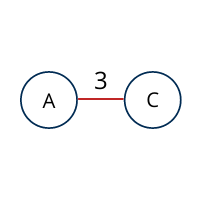
The least cost is 3 and the edges involved is AC. We add them. Adding them does not violate spanning-tree properties, so we continue to our next edge selection.
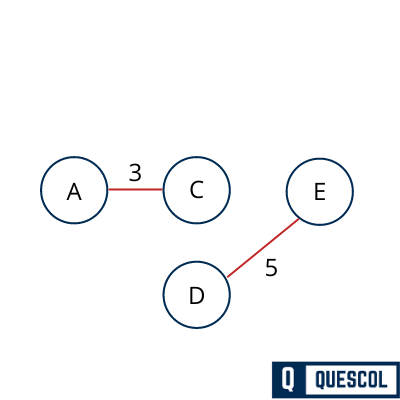
Next we will select Edge DE which have least weight 5 and not violating spanning tree properties.
Next we will select Edge AB which have least weight 7 and not violating spanning tree properties.
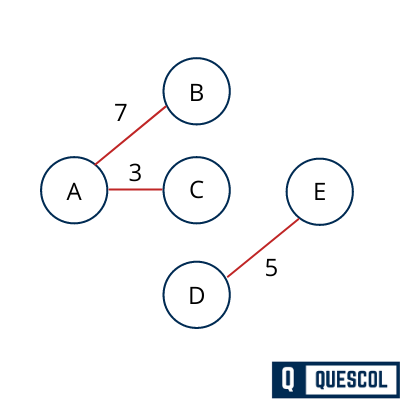
Next we will select Edge CE which have least weight 7 and not violating spanning tree properties.
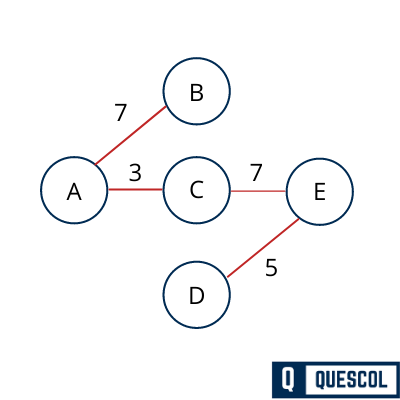
So Create Minimum spanning tree using Kruskal’s algorithm will look like above.
Time Complexity Analysis of Kruskal’s algorithm
Time Complexity : O(ElogE) or O(ElogV)
- Sorting of edges takes O(ELogE) time.
- After sorting, we iterate through all edges and apply find-union algorithm.
- The find and union operations can take at most O(LogV) time.
- So overall complexity is O(ELogE + ELogV) time.
- The value of E can be at most O(V2), so O(LogV) is O(LogE) the same.
- Therefore, the overall time complexity is O(ElogE) or O(ElogV)