Prim’s Algorithm Explanation with Example

by

Prim’s algorithm uses the greedy approach to find a minimum cost spanning tree for a connected weighted undirected graph. The algorithm builds a tree that includes all vertex and a subset of the edges in such a way that the sum of all the edges weight in the tree is minimum.

The major approach for the prims algorithm is finding the minimum spanning tree by the shortest path first algorithm. This algorithm adds new nodes from the Graph which has minimum edge weight to build a minimum spanning tree.

How Prim’s Algorithm works

Prim’s algorithm follows greedy algorithm to find minimum spanning tree. In greedy algorithm, it always choosing the next piece that offers the most local optimal solution of the problems where choosing locally optimal also leads to global solution.

We start from one vertex and keep adding next vertices that is connected with the lowest edge weight until we reach our goal.

The steps for implementing Prim’s algorithm are as follows:

  • Remove all loops and parallel edges.
  • Initialize the minimum spanning tree with any vertex of the graph.
  • Find all the edges that connect the tree to new unvisited vertices, find the minimum edges and add them to the tree.
  • Repeat step 2 until we get a minimum spanning tree.

Lets See an Example to understand Prim’s Algorithm

Prim's Algorithm

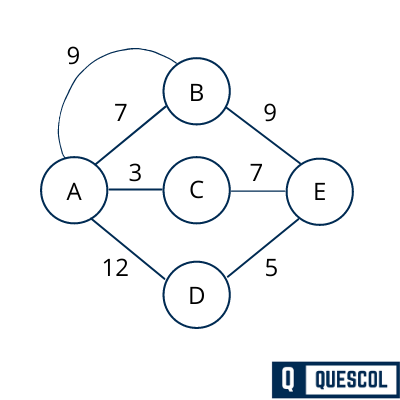
Step 1 – Remove all loops and parallel edges

After removing parallel edge from the graph, graph will look like below.

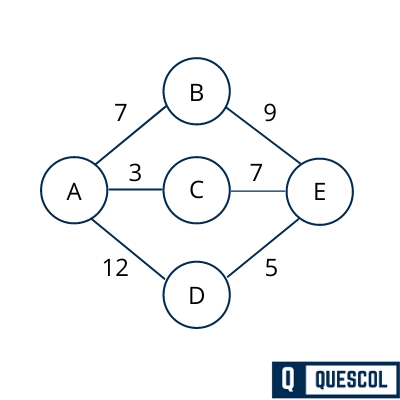
Prim's Algorithm

Step 2 – Choose any vertex for minimum spanning tree

In this case, we choose A vertex as the root node for Prim’s minimum spanning tree. You can choose any vertex and intialize it as minimum spanning tree node when next vertex with minimum weight will be added.

Step 3 – Find all outgoing edges from the selected vertex and select the one with less cost

After choosing the A as root node, we see that (A,B), (A,C) and (A,D) are three edges with weight 7, 3, and 12, respectively. We choose the edge (A,C) as it has the minimum edge weight.

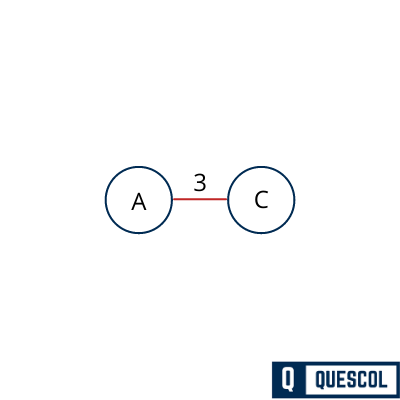
Now, the tree A-3-C is treated as one node and we check the all outgoing edges from A and C to find the minimum cost edge.

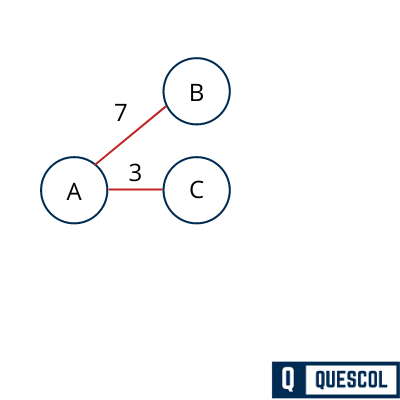
Here we found (A,B) and (C,E) has same weight. So we can select both.

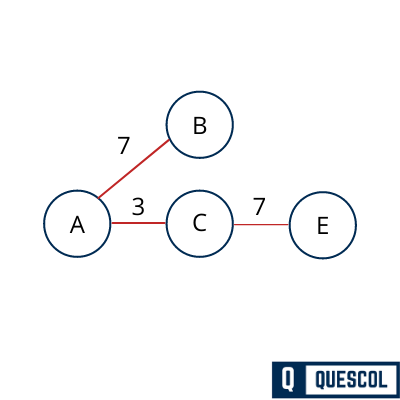
Now again find the all connected outgoing edges from the visited vertex to find the minimum cost edge. Here we got (E,D) has minimum edge weight so we will add (E,D) in the tree.

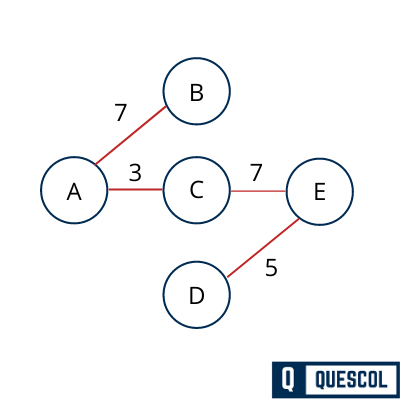
So this is the final minimum spanning tree with weight total edge weight 22.

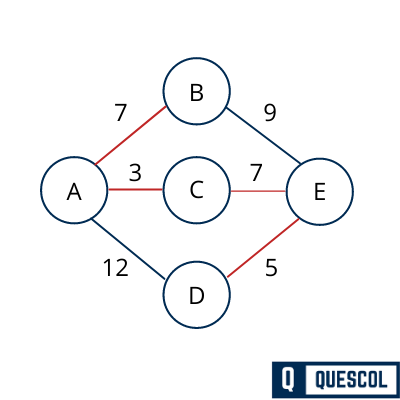
So this is how minimum spanning tree is created using prims algorithm from the graph.

Time Complexity Analysis of Prim’s Algorithm

Worst Case Time Complexity for Prim’s Algorithm is: –

  • O(ElogV) using binary Heap
  • O(E+VlogV) using Fibonacci Heap

All the vertices are needed to be traversed using Breadth-first Search, and then it will be traversed O(V+E) times. Min heap operation is used that decided the minimum element value taking of O(log V) time. So the merger of both will give the time complexity as O(Elogv) as the time complexity.

Advantages of Prim’s Algorithm

  1. Cost Efficiency: It minimizes the total weight (cost, distance, or time) of the spanning tree, ensuring the most economical way to connect all points in a network.
  2. Simplicity: Prim’s algorithm is straightforward to implement, making it accessible for various applications.
  3. Flexibility: It works well with both dense and sparse graphs, making it versatile for different network topologies.
  4. Optimality: Guarantees to find the minimum spanning tree (MST) of a connected, undirected graph, ensuring the best possible outcome.

Real-Time Applications of Prim’s Algorithm

  1. Telecommunications: Used in designing and optimizing the layout of networks to minimize the total length of cables needed to connect various nodes.
  2. Urban Planning: Helps in planning roads, water supply networks, and other infrastructure projects to ensure cost-effective and efficient layouts.
  3. Electrical Networks: Applied in designing electrical distribution systems to ensure minimal wiring length and cost.
  4. Computer Networks: Utilized in the layout of network cabling and routing to ensure efficient data transmission paths.
  5. Geographical Mapping: Aids in creating efficient routes for transportation and logistics, minimizing travel distances and costs.