Dijkstra’s algorithm, given by a brilliant Dutch computer scientist and software engineer Dr. Edsger Dijkstra in 1959. Dijkstra’s algorithm is a greedy algorithm that solves the single-source shortest path problem for a directed and undirected graph that has non-negative edge weight.
For Graph G = (V, E)
w (u, v) ≥ 0 for each edge (u, v) ∈ E.
This algorithm is used to find the shortest path in Google Maps, in network routing protocols, in social networking applications, and also in many places.
For a given graph G Dijkstra’s algorithm is helpful to find the shortest path between a source node to a destination node.
For example, if we draw a graph in which nodes represent the cities and weighted edges represent the driving distances between pairs of cities connected by a direct road, then Dijkstra’s algorithm when applied gives the shortest route between one city and all other cities. This algorithm is also used in GPS devices to find the shortest path between the current location and the destination. It has broad applications in industry, specially in domains that require modeling networks.
Dijkstra’s algorithm differs from the minimum spanning tree because the shortest distance between two vertices might not include all the vertices of the graph.
Dijkstra’s Algorithm
- Create a set sptSet (shortest path tree set) that keeps track of vertices included in shortest-path tree, i.e., whose minimum distance from the source is calculated and finalized. Initially, this set is empty.
- Assign a distance value to all vertices in the input graph. Initialize all distance values as INFINITE. Assign distance value as 0 for the source vertex so that it is picked first.
- While sptSet doesn’t include all vertices
- Pick a vertex u which is not there in sptSet and has a minimum distance value.
- Include u to sptSet.
- Update distance value of all adjacent vertices of u. To update the distance values, iterate through all adjacent vertices. For every adjacent vertex v, if the sum of a distance value of u (from source) and weight of edge u-v, is less than the distance value of v, then update the distance value of v. (Algo source : geeksforgeeks.com )
Lets see an example to understand Dijkstra’s Algorithm
Below is a directed weighted graph. We will find shortest path between all the vertices using Dijkstra’a Algorithm.
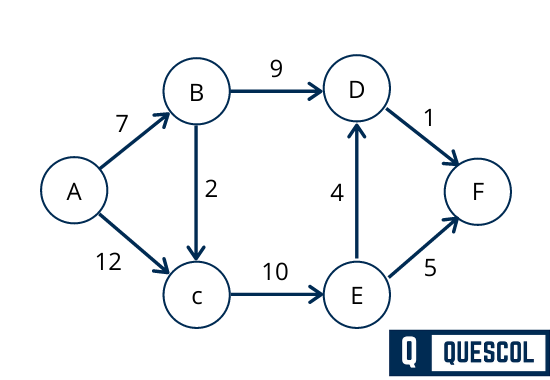
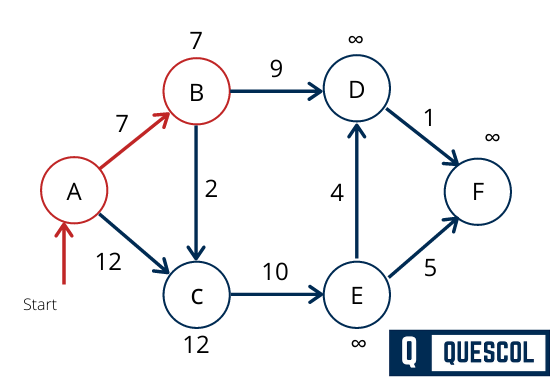
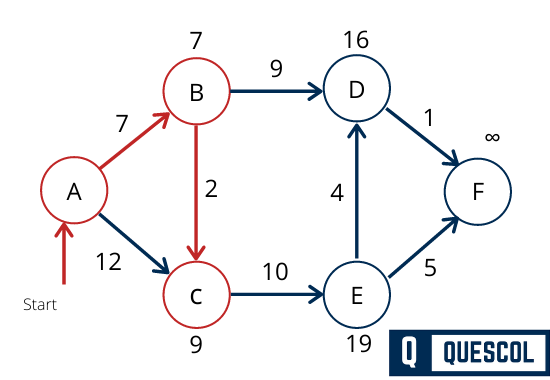
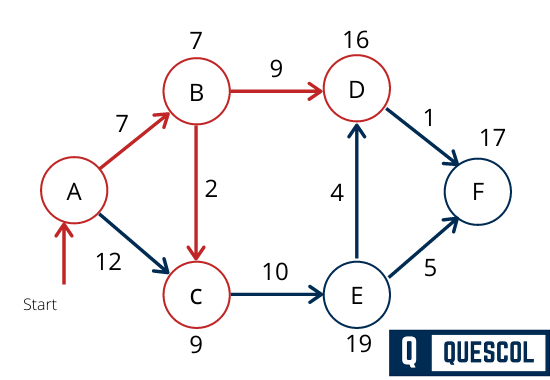
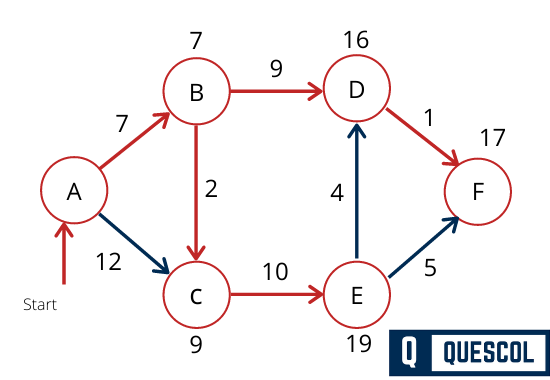
Dijkstra’s Algorithm Applications
- To find the shortest path between source and destination
- In social networking applications to map the connections and information
- In networking to route the data
- To find the locations on the map
Disadvantage of Dijkstra’s Algorithm
- It follows the blind search, so wastes a lot of time to give the desired output.
- It Negative edges value cannot be handled by it.
- We need to keep track of vertices that have been visited.
