What is Spanning Tree?
A spanning tree of a graph G is a subgraph of G that is a tree that includes all of the vertices of G and a minimum number of edges. A spanning tree does not contain any cycles and all the vertices should be connected.
For every connected and undirected graph there is at least one spanning tree.
Example of spanning tree
Suppose we have a graph containing V vertices and E edges. We can denote it as G(V,E)
Below is a undirected connected graph
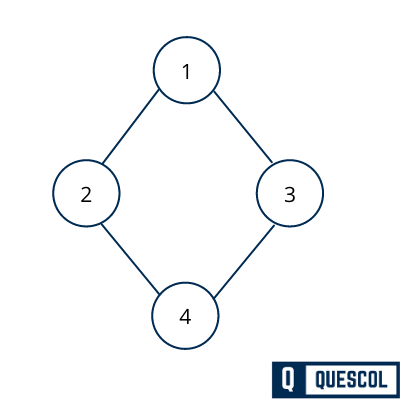
The spanning tree of the above graph should have all vertices, but the edges are not equal. The number of edges in the spanning tree would be equal to the number of vertices in the graph minus 1.
Spanning tree of graph G(V,E) is represented as:
G(V, E`)
where,
V=V`
E`ϵ E -1
E`=|V| – 1
Lets understand with the help of below example

Here we are going to create spanning tree of the below graph
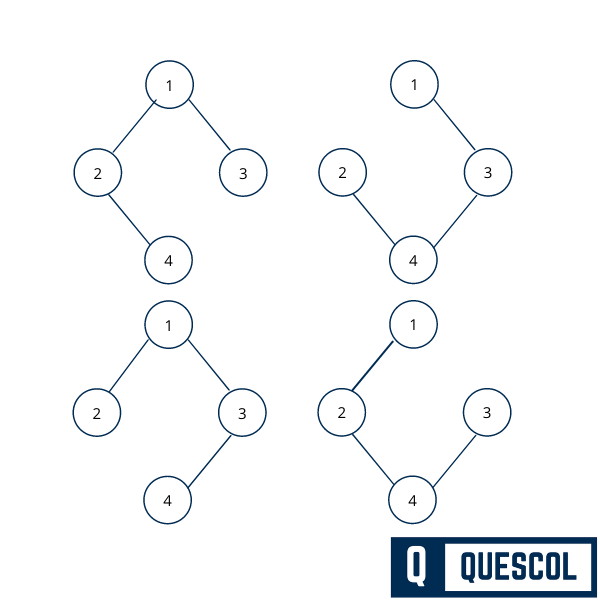
Properties of Spanning Tree
From the above example, We understand that a graph can have more than one spanning tree. Below are a few properties of the spanning tree −
- A connected graph G can have more than one spanning tree.
- All possible spanning trees of the graph has the same number of vertices and edges.
- Spanning tree does not contain any loops/cycles.
- If we remove any one edge from the spanning tree, the graph becomes disconnected.
- If we add anyone edge to the spanning tree, it will create a circuit or loop in the graph. So we can say that the spanning tree is maximally acyclic.
- For n vertices, A Spanning tree has n-1 edges.
- A complete graph can have a maximum n^n-2 number of spanning trees.
Minimum Spanning Trees
The minimum spanning tree of any connected weighted undirected graph is the tree whose sum of the weights of edges is minimum.
Example of Minimum Spanning Trees
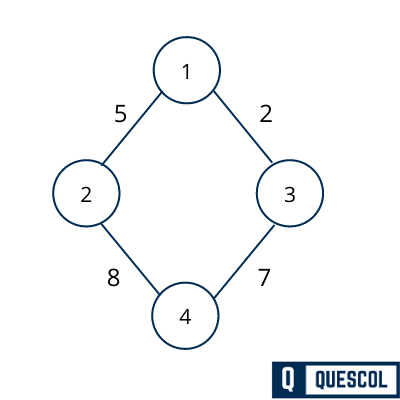
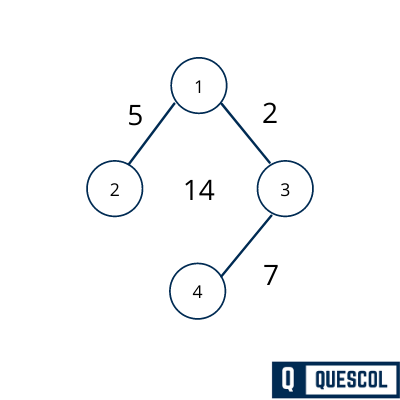
Here we are going to find minimum spanning tree for the below graph. There are more than one spanning tree can be formed using below graph. but only one will be minimum spanning tree.
We have created 4 spanning trees from the above-weighted graph. But their sum of weight will be different. Below all the 4 spanning graph has a different sum of weight 15, 17, 14, 20. But the spanning tree that has a minimum sum of edges will be a minimum spanning tree. Here 14 is the minimum so the tree with edge sum of 14 will be the minimum spanning tree.
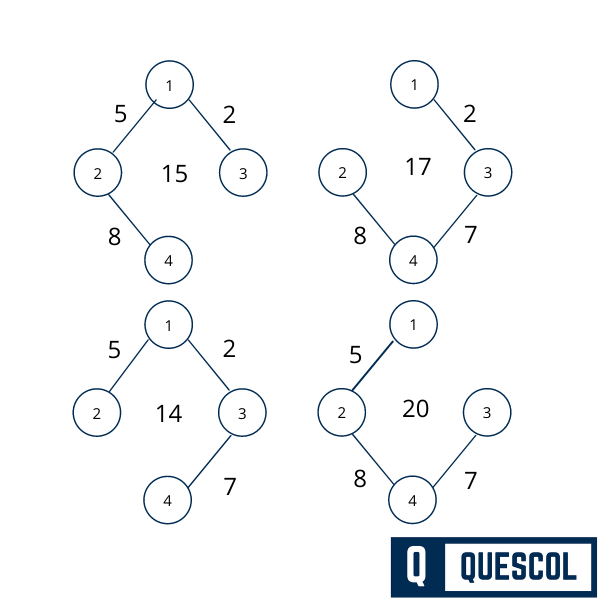
Minimum spanning tree
Minimum Spanning-Tree Algorithm
The two most important Minimum Spanning-Tree Algorithm are
- Kruskal’s Algorithm
- Prim’s Algorithm
Both are greedy Algorithms
Application of Minimum Spanning Tree
- Cluster Analysis
- Handwriting recognition
- Image segmentation
- Civil Network Planning
- Computer Network Routing
Application of MST in detail
- Minimum Spanning Tree are widely used for designing networks. For example, we can take the telephone, people separated by distances and they are connected together through a telephone network. A minimum spanning
the tree is used to determine the least costly paths without any cycles in this network.
- MSTs are used to find airline routes that have the least cost with no cycles. Here cities are denoted by vertices and edges represent the routes between these cities.
Difference Between Spanning tree and Minimum Spanning tree
spanning tree vs minimum spanning tree
| Spanning Tree | Minimum Spanning Tree |
|---|---|
| Connects all vertices in a graph. | Connects all vertices in a graph. |
| May not have the minimum possible weight sum of all its edges. | Has the minimum weight sum of all its edges. |
| Any acyclic connected subgraph that includes all vertices can be a spanning tree. | Is a spanning tree with the smallest possible total edge weight. |
| There can be many spanning trees for a single graph. | There is at least one minimum spanning tree for a connected weighted graph, but there can be multiple if the smallest weights are the same for different configurations. |
| Does not necessarily consider the weights of the edges. | Is formed considering the edge weights to ensure the minimum total cost. |
| Used when simply connectivity of all points is the goal. | Used in applications like network design, where cost, length, or another weight is a factor. |
