Column Major Order is a way to represent the multidimensional array in sequential memory. It has similar functionality as row-major order, but the way of process is different.
In Column Major Order, elements of a multidimensional array are arranged sequentially column-wise which means filling all the index of the first column and then move to the next column.
Let’s see an example
Suppose we have some elements {1,2,3,4,5,6,7,8} which we want to insert in an array by following column-major order.
So If we insert these elements in column-major order, our 2-D array will look like
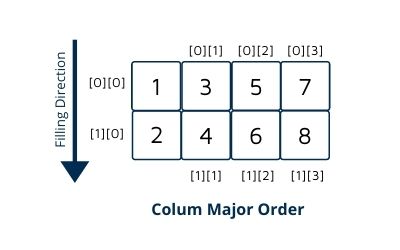
Here first fill index[0][0] and then index[1][0] which is just opposite to the row-major where we first fill all row nodes then move to the next row.
And then for second-column index[0][1] and then index[1][1], index[0][2], index[1][2] and so on.
Why Use Column Major Order?
This order is crucial in programming and data structure because it affects how quickly and efficiently a computer can access and process data. In column major order, data that appears in the same column are stored close together in the computer’s memory. This closeness can speed up tasks that need to access this column data frequently.
Examples in Real Life
Imagine a classroom seating chart where students are listed by columns, starting from the front to the back, and then moving to the next column. If a teacher wants to call on students column by column for a quiz, this order makes it easy to see who’s next.
Column Major Order Formula
The Location of element A[i, j] can be obtained by evaluating expression:
LOC (A [i, j]) = base_address + w * [m * j + i]
Here,
base_address = address of the first element in the array.
w(Size of element) = Word size means a number of bytes occupied by each element of an Array.
m = Number of rows in the array.
i = is the row index.
j = is the column index.
Note: Array Index starts from 0.
Here we have taken a 2-D array A [2, 4] which has 2 rows and 4 columns.
Problem to solve on column major
Suppose we want to calculate the address of element A [1, 2] in column-major order and the matrix is 2*4. It can be calculated as follow:
Now to calculate the base address of any index using column-major order we can use the process given below.
It can be calculated as follow:
Here,
base_address = 2000, W= 2, M=2, i=1, j=2
LOC (A [i, j]) = base_address + W [M * j + i ]
LOC (A[1, 2]) = 2000 + 2 [2*2 + 1]
= 2000 + 2 * [4 + 1]
= 2000 + 2 * 5
= 2000 + 10
= 2010
Benefits in Math and Science
Column major order is particularly beneficial in fields like mathematics and scientific computing. Many mathematical operations, like matrix multiplication or solving systems of linear equations, can be optimized if the data is stored in this way. This is because accessing column data repeatedly is faster due to the way computer memory works.
Comparison with Row Major Order
It’s helpful to compare column major order with row major order, where data is filled row by row. Row major order is like reading a book from left to right, then top to bottom. Most programming languages, like C and Python, use row major order for arrays. The choice between row and column major order depends on how the data will be accessed and used. For some applications, column major order is more efficient, especially in matrix computations.
Choosing the Right Order
The decision to use column major order over row major order should be based on the specific needs of your project. If you’re working with matrices and find yourself accessing columns more often than rows, column major order could be the way to go. This choice can lead to faster, more efficient code, particularly in applications that require heavy mathematical computation.
Conclusion
Column major order is a powerful concept in data structure and programming, especially useful in mathematical and scientific computing. By storing data in a way that matches how it’s accessed, programs can run faster and more efficiently. Whether you’re a student, programmer, or scientist, understanding and utilizing column major order can significantly impact your work’s effectiveness and efficiency.
