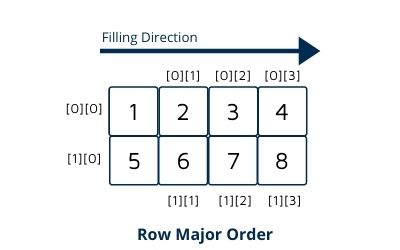
Row Major Order is a way to represent the elements of a multi-dimensional array in sequential memory. In Row Major Order, elements of a multi-dimensional array are arranged sequentially row by row, which means filling all the index of first row and then moving on to the next row.
Let’s see an example
Suppose we have some elements {1,2,3,4,5,6,7,8} to insert in array.
So If we insert these elements in row-major order, our 2-D array will look like
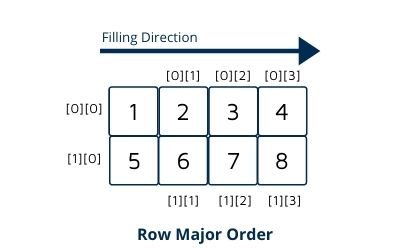
Here first fill index[0][0] and then index[0][1]
And for second-row index[1][0] and then index[1][1] and so on
Row Major Order Formula
Row Major Order Formula is used to calculate the memory address of a given array index location.
The Location of element A[i, j] can be obtained by evaluating the expression:
LOC (A [i, j]) = base_address + W [N * i + j]
Here,
base_address = address of the first element in the array.
W(Size of element) = Word size, means a number of bytes occupied by each element of an Array. It depends on the data type, e.g., 4 bytes for an int in many systems.
M = Number of rows in the array.
Note: Array Index starts from 0.
i = is the row index
j = is the column index
Problem to solve on row major
Suppose we want to calculate the address of element A [1, 2] and the matrix is of 2*4. It can be calculated as follow:
Here,
base_address = 1000, W= 2, M=2, i=1, j=2
LOC (A [i, j]) = base_address + W * [(N*i) + j]
LOC (A[2, 3]) = 1000 + 2 *[4*(1) + 2]
= 1000 + 2 * [4 + 2]
= 1000 + 2 * 6
= 1000 + 12
= 1012
Row Major Order Examples
2-D Array Example
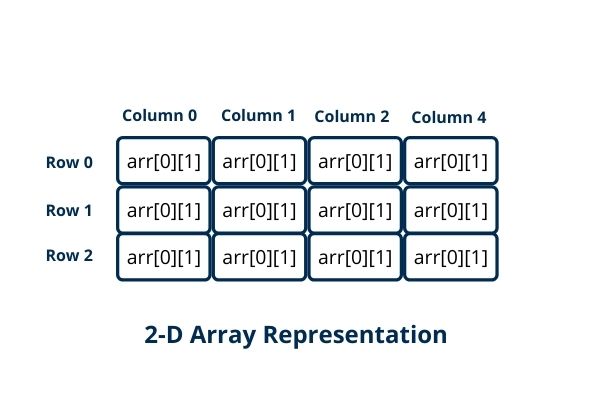
2-D array in C
int A[2][4] = {
{1, 2, 3, 4},
{5, 6, 7, 8}
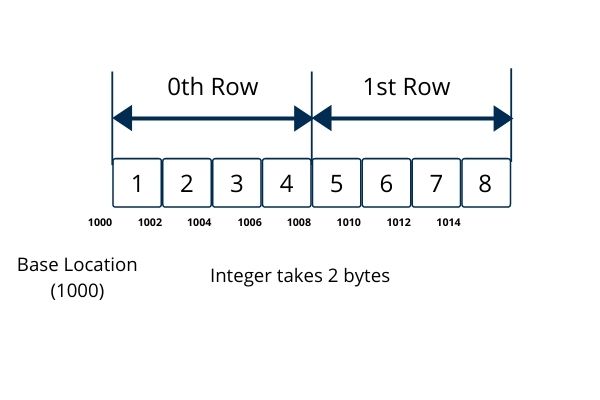
};Above 2-D Array Will look Like
We have a 2*4 matrix it means our matrix has 2 rows and 4 columns
Memory Representation of 2-D array in Row Major Order
3-D Array Example
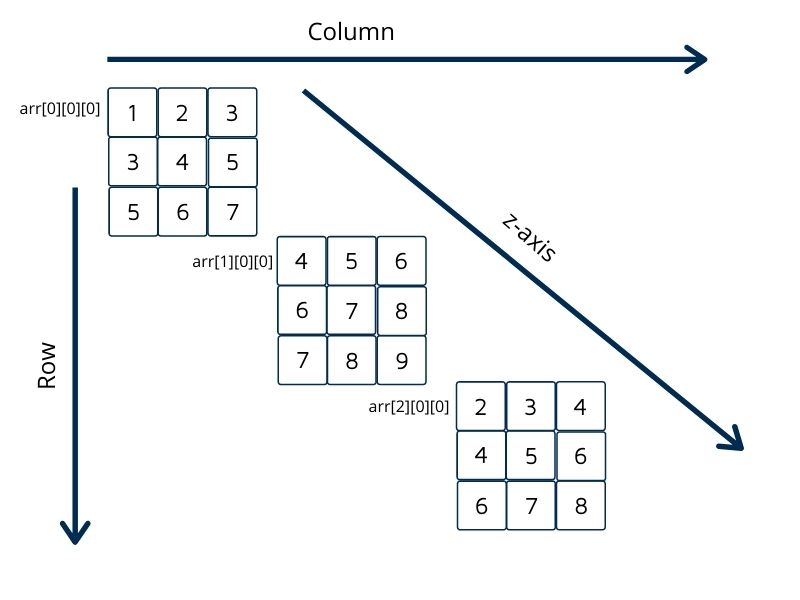
3-D array in C
int A[3][3][3] = {
{
{1,2, 3}, {3,4,5}, {5,6,7}
},
{
{4,5,6}, {6,7,8}, {7,8,9}
},
{
{2,3,4}, {4,5,6}, {6,7,8}
}
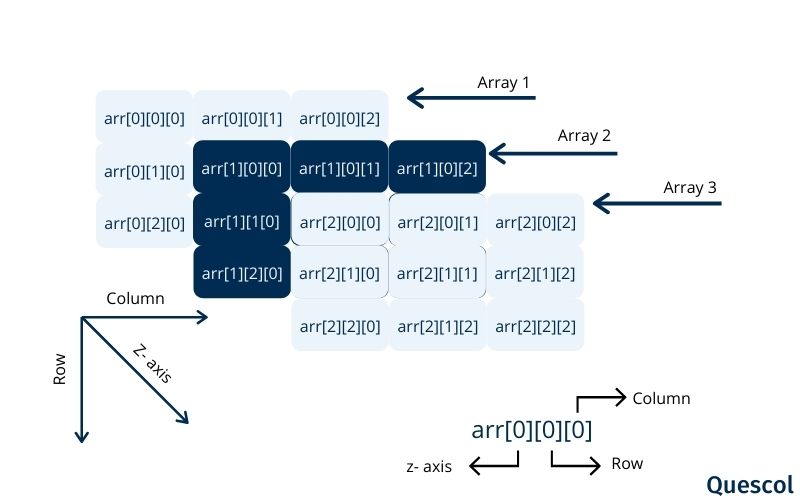
};Above Array Will look Like
In this example, we will see a 3-D matrix or 3-dimensional array. We have a 3*3*3 matrix.