Sparse Matrix and its representation with example

by

Matrix is defined with a 2-dimensional array that has row and column. An array which has ‘m’ rows and ‘n’ columns represent an mXn matrix.

Sometimes it happens when a matrix has zero values is more than NON-ZERO values.

The matrix which has a greater number of zero values in comparison to the non-zero values is known as a sparse matrix.

What is Sparse Matrix?


A sparse matrix is a matrix in which most of the elements are zero. In details we can say that it is a dense matrix in which most of the elements are non-zero. Sparse matrices frequently arise in various fields such as scientific computing, data analysis, and graph theory.

For Example

What is Sparse Matrix

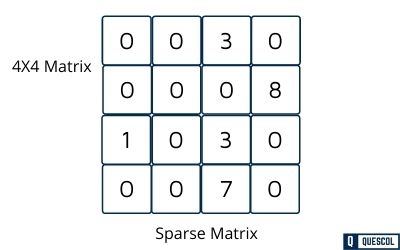
In the above example we have 4 X 4 matrix where only 5 values are non-zero and rest of the value are zero.

So if we calculate the space

Integer value takes 2 bytes

Total space taken by 4 X 4 matrix is 4 X 4 X 2 = 32 bytes.

Where only 5 X 2 = 10 bytes are in use which has a non-zero value and the rest 32 – 10 = 22 bytes are wastage of memory. This can also be less.

But if we have large number of data in matrix like there is a matrix of size 100 X 100 which contains only 10 non-zero elements and 90 zero elements.
So from the above scenario, it is visible that only 10 spaces are filled with non-zero values, and the remaining spaces of a matrix are filled with zero values.

This matrix will take a total of 100 X 100 X 2 = 20000 bytes of space to store this integer matrix. And to search these 10 non-zero elements, we have to scan all elements of this matrix 10000 times.
Now to save the memory and searching time, we use Sparse matrix representation.

Loss of memory is high when we represent the sparse matrix with the help of a 2-dimensional array.

We can overcome this situation and can save money by the following representation explained below.

Sparse Matrix Representations

A sparse matrix can be represented in two way:

1. Triplet Representation

2. Linked Representation

1. Triplet Representation

In Triplet Representation of a sparse matrix, we consider only non-zero values along with their row and column index values. The 0th row of the matrix stores the total number of rows, total number of columns, and total non-zero values.
For example, consider a matrix of size 4 X 4 containing 5 number of non-zero values.

Sparse matrix representation in a data structure

sparse matrix in data structure
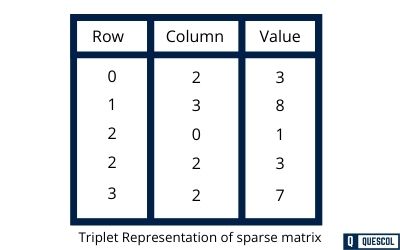
Triplet Representation

In the above example of the matrix, there are only five non-zero elements, those are 3, 8, 1, 3, 7, and matrix size is 4 X 4. We represent this matrix in triplet representation (row, column, value), as shown in the above image.

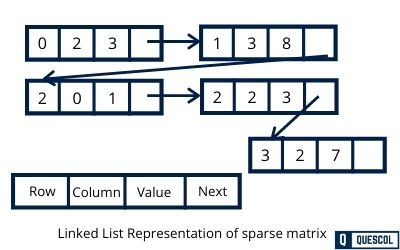
2. Linked Lists Representation

In linked list representation, we use a linked list to represent a sparse matrix. Each node of the linked list has four fields.

These four fields are defined as:

Row: Row keeps row index of a non-zero element

Column: Column keeps column index of a non-zero element

Value: non zero element located at (row,column) index

Next node: Next node, stores the address of the next node

sparse matrix in data structure
Linked Lists Representation

Why Sparse Matrix a better option over a Simple matrix?

It saves the memory only by storing non-zero elements when a non-zero element is lesser than zeros.
It saves Computing time because, in a sparse matrix, logically designed data structure traverses only non-zero elements.

Operations of Sparse Matrix

We can perform 3 operations on Sparse Matrix

1). Addition

When adding two sparse matrices, you only need to add the elements that have corresponding non-zero values in the same location in each matrix. Here’s a step-by-step description:

  1. Match Non-Zero Elements: First, find the elements in the same position in both matrices that are non-zero.
  2. Add Matching Elements: Add these matching non-zero elements together.
  3. Retain Unique Non-Zero Elements: Include non-zero elements that are unique to each matrix in their original position in the result matrix.
  4. Ignore Zeros: No need to add zero to zero, so those combinations are ignored.

Sparse Matrix Addition Example

Suppose we have two sparse matrices A and B, represented in tuple form:

  • Matrix A: [(0, 1, 5), (1, 2, 8)]
  • Matrix B: [(0, 1, 3), (2, 0, 7)]

The resulting matrix C after adding A and B:

  • Matrix C: [(0, 1, 8), (1, 2, 8), (2, 0, 7)]

Here, (0, 1, 8) is obtained by adding (0, 1, 5) from matrix A and (0, 1, 3) from matrix B. The other elements do not have corresponding elements with the same row and column indices, so they are copied as they are.

2). Multiplication

Multiplying sparse matrices is more complex than addition because you need to compute dot products that often involve zero and non-zero elements. The steps are:

  1. Row by Column Dot Product: For each row of the first matrix, compute the dot product with each column of the second matrix.
  2. Multiply Non-Zero Pairs: When the row element and the corresponding column element are both non-zero, multiply them.
  3. Sum Products for Each Position: The sum of these products gives you one element of the resulting matrix.
  4. Build Result Sparse Matrix: Construct the resulting sparse matrix by placing the sums in their corresponding positions.
  5. Optimize Computation: Skip the multiplication and addition involving zeros, which is what makes sparse matrix multiplication computationally efficient.

Sparse Matrix Multiplication Example

Let’s multiply two sparse matrices A and B:

  • Matrix A: [(0, 0, 1), (1, 1, 1)] (This is an identity matrix in sparse format)
  • Matrix B: [(0, 1, 4), (1, 0, 5)]

For multiplication, we perform the dot product of rows of A with columns of B. Since A is an identity matrix, the resulting matrix C will simply be the same as matrix B:

  • Matrix C: [(0, 1, 4), (1, 0, 5)]

In a more complex case where the matrices are not identity matrices, you would sum the products of elements where the column index of A matches the row index of B.

3). Transpose

Transposing a sparse matrix involves flipping the matrix over its diagonal, which means the row and column indices of all non-zero elements are swapped. Here’s how it’s done:

  1. Swap Indices: Convert each non-zero element’s position from (row, column) to (column, row).
  2. Retain Values: Keep the non-zero values the same, but place them in the swapped positions in the new matrix.
  3. Reformat if Needed: Depending on the storage format (like CSR or CSC), you may need to reformat the matrix to ensure it’s still stored efficiently.

Sparse Matrix Transpose Example

Consider a sparse matrix A:

  • Matrix A: [(0, 2, 3), (1, 1, 5), (2, 0, 9)]

To transpose, we swap the row and column indices of every element:

  • Transposed Matrix A: [(2, 0, 3), (1, 1, 5), (0, 2, 9)]