Breadth-first search graph traversal techniques use a queue data structure as an auxiliary data structure to store nodes for further processing. The size of the queue will be the maximum total number of vertices in the graph.
It is a smart way to look through data organized in a graph. A graph is a collection of points (called nodes or vertices) connected by lines (called edges).
How BFS Works?
- Starting Point: Pick a node to start from. This is like choosing where to enter the garden maze.
- Exploring Nearby: Look at all the nodes directly connected to your starting point. This is like checking all the paths that branch off from where you’re standing.
- Moving Outward: Once you’ve checked all the nearby nodes, move on to the next set of nodes that are one step farther away.
- Repeat: Keep going, exploring nodes farther and farther out, until you’ve visited every node.
Steps to implement BFS traversal
Step 1 – First define a Queue of size n. Where n is the total number of vertices in the graph.
Step 2 – Select any vertex which is a starting point from where traversal will start.
Step 3 – Visit starting vertex and insert it into the Queue.
Step 4 – Visit all the non-visited adjacent vertices which is connected to it and insert all non-visited vertices into the Queue.
Step 5 – When there is no new vertex to be visited from the element which is top in a queue, Remove the top element which is the vertex from the queue.
Step 6 – Repeat steps 4 and 6 until the queue becomes empty.
Step 7 – When all elements removed from the queue, then produce the final spanning tree by removing unused edges from the graph.
Example Of BFS Graph Traversal
Initialize the queue
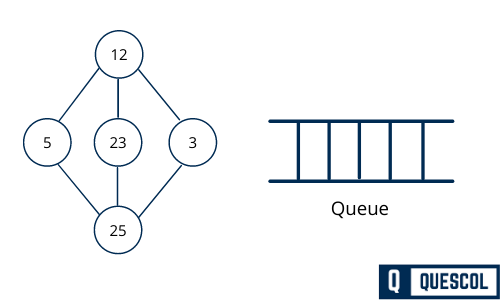
We start visiting from vertex 12 that can be considered as starting node, and mark it as visited.
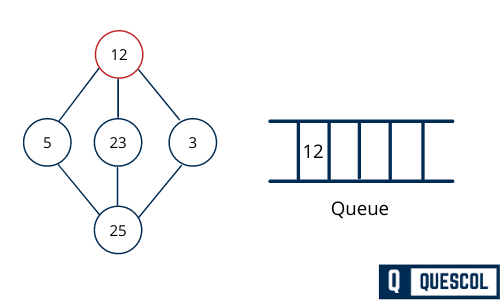
Now we will see an unvisited adjacent node from 12. In this example, we have three nodes and we can visit anyone. here we are traversing from left to right. We choose 5 and mark it as visited and enqueue it.
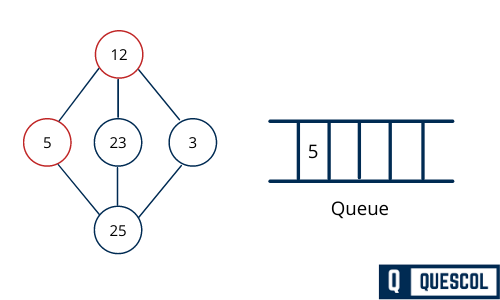
Next, visit the unvisited adjacent node from 12 to 23 . We mark it as visited and enqueue it.
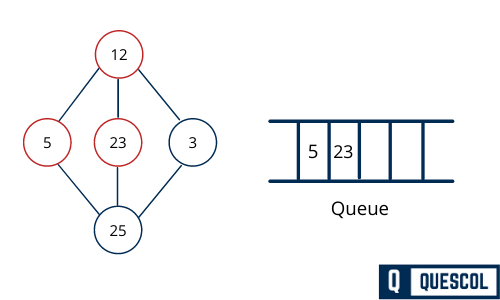
Next, the unvisited adjacent node from 12 is 3. We mark it as visited and enqueue it.
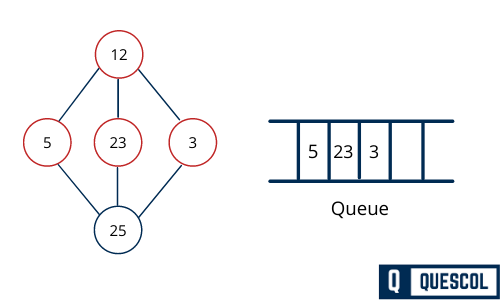
Now, all the connected adjacent node from 12 is traversed and no unvisited adjacent nodes left. So, we dequeue and find all connect vertex from 5.
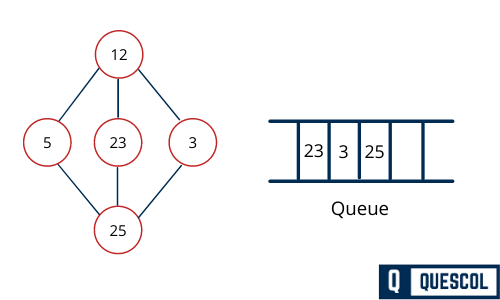
From 5 we have 25 as unvisited adjacent node. We mark it as visited and enqueue it.
Now if all nodes visited, we will dequeue all nodes from queue.
So BFS Traversal output is : 12, 5, 23, 3, 25
Complexity Analysis of BFS
Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Space Complexity: O(V).
Since, an extra visited array is needed of size V.
Applications of BFS
- Finding the Shortest path in an unweighted graph
- Find a solution to a game with the least number of moves. In such a scenario each state of the game can be represented by a node and state transitions as edges
- Finding Connected Components in an unweighted graph
- Level Order Traversal in Tree
- Find the shortest paths in graphs with weights 0/1
Conclusion
Breadth First Search is a powerful tool for exploring and finding things in graphs, from solving puzzles and mazes to navigating maps and social networks. It’s like having a map and a strategy, ensuring you explore every nook and cranny in the most efficient way possible. Whether in games, online, or in real-world problems, BFS helps us find our way, connect the dots, and discover solutions one step at a time.
