A graph is a non-linear data structure that consists of vertices and edges.
Vertices are also known as nodes. Edges can be in order or not. An ordered pair (u, v) indicates that there is an edge from vertex u to vertex v in a directed graph. Also in directed graph (u,v) is not equal to (v,u).
An undirected graph (u,v) is equal to (v,u) because there is no direction. The edges of the graph may have weight/value/cost.
Graphs data structure has many real world applications. For an example Graphs are used to represent paths in a city in maps or internet network. Graphs are also used in social networks systems like linkedIn, Facebook, Instagram.
In social networks systems for example, in Facebook, each person represented with a vertex(or node). And another node contains information like person id, name, gender, and locale which is connected by edges.
Graph representation means the ways of storing graphs in the computer’s memory.
There are two types of graph representation
1). Adjacency matrix representation
2). Adjacency list representation
1). Adjacency matrix representation
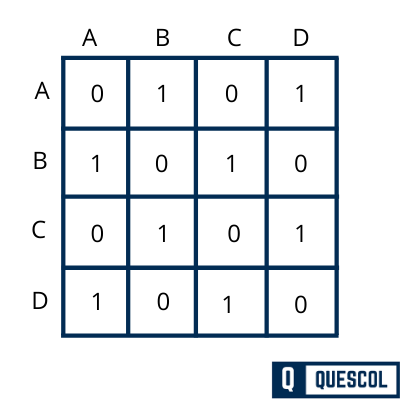
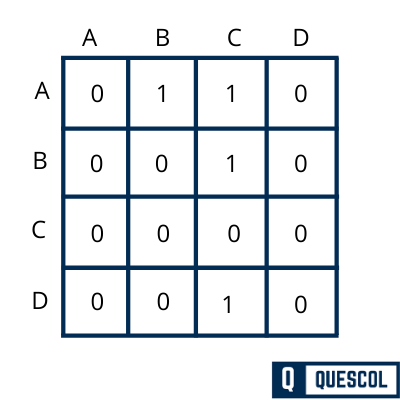
An adjacency matrix is used to represent adjacent nodes in the graph. Two nodes are said to be adjacent if there is an edge connecting them. We represent graph in the form of matrix in Adjacency matrix representation. For a graph G, if there is an edge between two vertices a and b then we denote it 1 in matrix. If there is no edge then denote it with 0 in matrix.
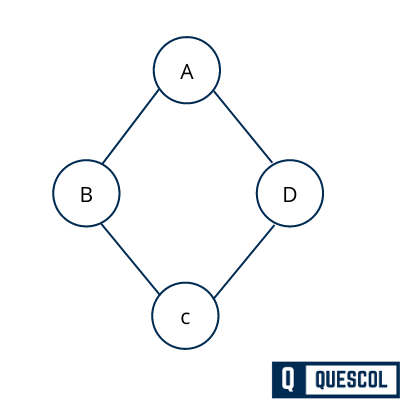
For Un-Directed graph
Mi,j = 1 if there is an edge between vertex i and j. The direction does not matter here.
and Mi,j = 0 if there is no edge between vertex i and j.
Mi,j not equal to Mj,i
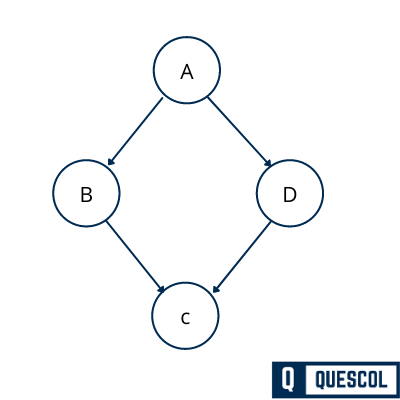
For Directed graph
Mi,j = 1 if there is an edge starting from vertex i and terminating at vertex j
and Mi,j = 0 if there is no edge starting from vertex i and terminating at vertex j.
Mi,j not equal to Mj,i
Adjacency matrix gives us constant time and all-time access to running time (O(1) ) that helps to find out if any edge exists between two given nodes. The space complexity is given by O(V2).
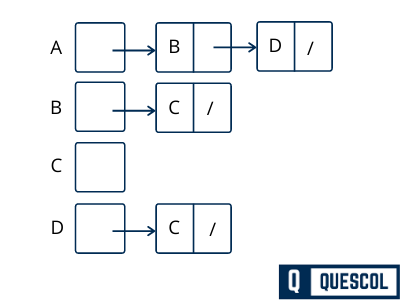
2). Adjacency list representation
An adjacency list is another way to represented a graph in the computer’s memory. This structure consists of a list of all nodes in G. Every node is in turn linked to its own list that contains the names of all other nodes that are adjacent to it.
Lets see below example to understand it
Adjacency list representation of Un-directed graph

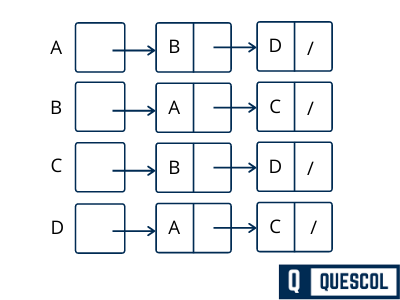
Adjacency list representation of directed graph