DFS stands for Depth First Search, is one of the graph traversal algorithms that uses Stack data structure. In DFS Traversal go as deep as possible of the graph and then backtrack once reached a vertex that has all its adjacent vertices already visited.
Depth First Search (DFS) algorithm traverses a graph in a depthward motion and uses a stack data structure to remember to get the next vertex to start a search, when a dead end occurs in any iteration.
DFS traversal for tree and graph is similar but the only difference is that a graph can have a cycle but the tree does not have any cycle. So in the graph we have additional array which keeps the record of visited array to protect from infinite loop and not visited again the visited node.
How Does DFS Work?
DFS starts at a selected node (or root in a tree) and explores as far as possible along each branch before backtracking. This process uses a stack, either through the function call stack via recursion or an explicit stack data structure, to keep track of the path.
Key Points in DFS
- Exploration: DFS goes deep into the graph, following one path until it can’t go any further.
- Backtracking: When it reaches the end of a path, DFS backtracks to explore new paths.
- Uses a Stack: DFS uses a stack to remember where it needs to return to once it reaches a dead end.
Steps to implement Depth First Traversal
Step 1 – Visit all adjacent unvisited vertex. Mark it as visited. Print it and Push it in a stack.
Step 2 − If no adjacent vertex is found, pop up a vertex from the stack.
Step 3 − Repeat Step 1 and Step 2 until the stack is empty.
Graph Traversal using DFS Technique
Initialize the stack
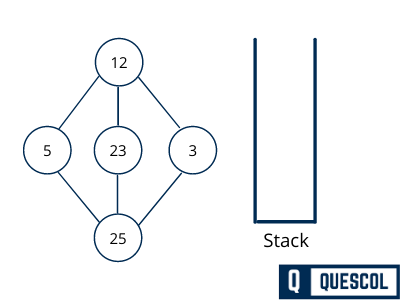
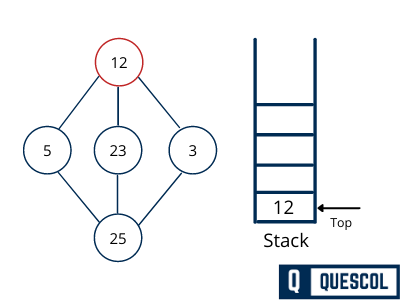
Mark 12 as visited and push into stack. Now Explore any unvisited adjacent node from 12. In our example We have three nodes. We can pick any of them. Here we are going to pick 5.
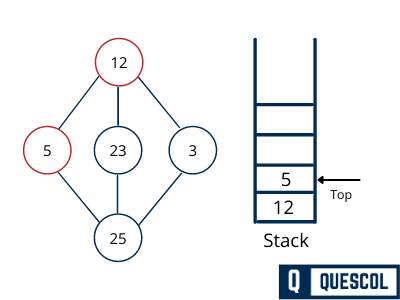
Mark 5 as visited and put it onto the stack. Explore any unvisited adjacent node from 5. Both 12 and 25 are adjacent to 5 but we are concerned for unvisited nodes only.
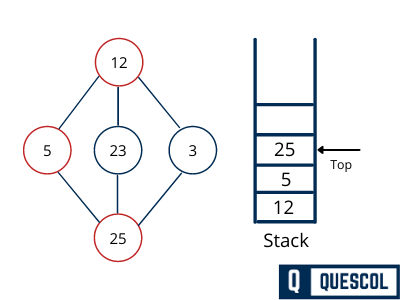
Visit 25 and mark it as visited and put onto the stack. Here, we have 23 and 3 nodes, which are adjacent to 25 and both are unvisited.
We choose 3, mark it as visited and put onto the stack. Here 3 does not have any unvisited adjacent node. So, we pop 3 from the stack.
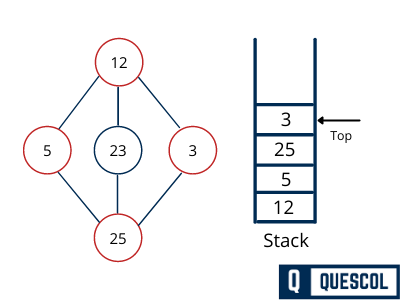
We check the stack top for return to the previous node and check if it has any unvisited nodes. Here, we find 25 to be on the top of the stack.

Only unvisited adjacent node is from D is 23 now. So we visit 23, mark it as visited and put it onto the stack.
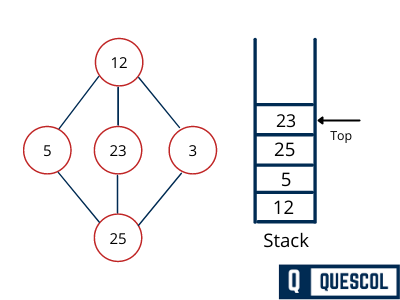
Output of DFS Traversal will be : 3, 23, 25, 5, 12
Complexity Analysis
Time complexity: O(V + E), where V is the number of vertices and E is the number of edges in the graph.
Space Complexity: O(V).
Since, an extra visited array is needed of size V.
DFS Variants
There are variations to how DFS can be applied, based on the specific needs of the task:
- Pre-order: Visit the node as soon as you see it.
- In-order: Visit the node after you’ve explored its left child but before exploring its right child (mainly in binary trees).
- Post-order: Visit the node after you’ve explored all its children.
Application of DFS
- Find a path from the source vertex to other vertices
- Find the connected components in a graph
- Topological Sorting
- Find bridges and articulation points in a graph
- Find LCA of two nodes in a graph
- Find cycles in a directed and undirected graph
C Program to Implement DFS
#include<stdio.h>
#include<stdlib.h>
// Adjusting the maximum limit for graph vertices
#define VERTICES_LIMIT 5
// Structure for the adjacency list nodes
typedef struct Node {
int vertexID;
struct Node* linkNext;
} Node;
// Structure representing the entire graph
typedef struct UniqueGraph {
int totalVertices;
Node** adjListArray;
int* visitedNodes;
} UniqueGraph;
// Function to craft a new node for the adjacency list
Node* initiateNode(int vertex) {
Node* freshNode = (Node*)malloc(sizeof(Node));
freshNode->vertexID = vertex;
freshNode->linkNext = NULL;
return freshNode;
}
// Graph initialization function
UniqueGraph* createGraph(int vertices) {
UniqueGraph* newGraph = (UniqueGraph*)malloc(sizeof(UniqueGraph));
newGraph->totalVertices = vertices;
newGraph->adjListArray = (Node**)malloc(vertices * sizeof(Node*));
newGraph->visitedNodes = (int*)malloc(vertices * sizeof(int));
for (int i = 0; i < vertices; i++) {
newGraph->adjListArray[i] = NULL;
newGraph->visitedNodes[i] = 0;
}
return newGraph;
}
// Adding edges to the graph
void insertEdge(UniqueGraph* newGraph, int origin, int destination) {
// Origin to destination
Node* newNode = initiateNode(destination);
newNode->linkNext = newGraph->adjListArray[origin];
newGraph->adjListArray[origin] = newNode;
// Since it's undirected, add edge back from destination to origin
newNode = initiateNode(origin);
newNode->linkNext = newGraph->adjListArray[destination];
newGraph->adjListArray[destination] = newNode;
}
// The DFS traversal implementation
void deepFirstSearch(UniqueGraph* newGraph, int startVertex) {
Node* list = newGraph->adjListArray[startVertex];
Node* traverse = list;
newGraph->visitedNodes[startVertex] = 1;
printf("Visited %d \n", startVertex);
while (traverse != NULL) {
int connectedVertex = traverse->vertexID;
if (newGraph->visitedNodes[connectedVertex] == 0) {
deepFirstSearch(newGraph, connectedVertex);
}
traverse = traverse->linkNext;
}
}
// Main function to demonstrate the DFS traversal
int main() {
UniqueGraph* myGraph = createGraph(VERTICES_LIMIT);
insertEdge(myGraph, 0, 1);
insertEdge(myGraph, 0, 2);
insertEdge(myGraph, 1, 2);
insertEdge(myGraph, 1, 3);
insertEdge(myGraph, 2, 4);
printf("Initiating Depth First Search from vertex 0:\n");
deepFirstSearch(myGraph, 0);
return 0;
}
Output
Initiating Depth First Search from vertex 0:
Visited 0
Visited 2
Visited 4
Visited 1
Visited 3 Explanations
The graph is represented using an adjacency list, a common method for storing graphs that lists all the vertices connected to each vertex. This representation is efficient in terms of space, especially for sparse graphs.
Key Components
- Node Structure (
Node): Represents an individual element in the adjacency list. EachNodecontains the ID of the vertex (vertexID) it represents and a pointer to the next node in the list (linkNext). - Graph Structure (
UniqueGraph): Represents the entire graph. It contains the total number of vertices in the graph (totalVertices), an array of pointers toNode(adjListArray) representing the adjacency list for each vertex, and an array (visitedNodes) to track which vertices have been visited during DFS traversal. - Function
initiateNode: Creates a new node for the adjacency list. It assigns the vertex ID and sets the next link toNULL. - Function
createGraph: Initializes a new graph with a specified number of vertices. It allocates memory for the graph structure, adjacency list array, and visited nodes array, setting initial values. - Function
insertEdge: Adds an undirected edge between two vertices in the graph by updating the adjacency lists of both vertices. It ensures the graph reflects the bidirectional nature of undirected edges. - Function
deepFirstSearch: Implements the DFS traversal logic. Starting from a given vertex, it marks the vertex as visited, then recursively visits all adjacent, unvisited vertices. The function uses thevisitedNodesarray to keep track of which vertices have been visited, preventing infinite loops in cyclic graphs. - Main Function (
main): Demonstrates how to use the program by creating a graph, adding edges to form a specific structure, and then performing a DFS traversal starting from vertex 0.
How DFS Works in This Program
- Initialization: The program begins by creating a graph with a predefined number of vertices using
createGraph. - Building the Graph: It then inserts edges between specific vertices using
insertEdgeto form the graph’s structure. - Performing DFS: Starting from vertex 0,
deepFirstSearchis called. This function:- Marks the starting vertex as visited.
- Recursively visits all adjacent vertices that haven’t been visited yet, following the depth-first principle.
