A sparse matrix is a type of matrix filled mostly with zeros. Think of a huge whiteboard where only a few spots are marked, and the rest is blank. There are several types of sparse matrices, but let’s talk about its types : lower triangular, upper triangular and Tri-diagonal sparse matrices.
Three types of Sparse Matrix
1). Lower triangular sparse matrix
2). Upper triangular sparse matrix
3). Tri-diagonal matrix
1. Lower Triangular Matrix / Sparse Matrix
In a Lower triangular sparse matrix, all elements above the main diagonal have a zero value. This type of sparse matrix is also known as a lower triangular matrix. If you see its pictorial representation, then you find that all the elements having non-zero value are appear below the diagonal.
In a lower triangular matrix, Arr i,j=0 where i<j.
A lower-triangular Matrix Arr of size n*n has one non-zero element in the first row, two non-zero elements in the second row, and similarly n non-zero elements in the nth row.
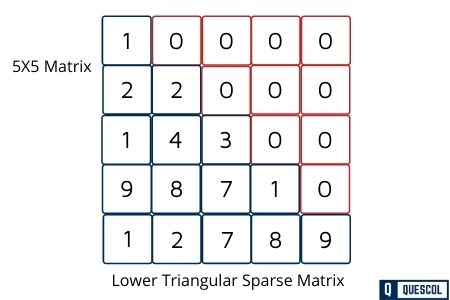
We use a one-dimensional array to store a lower-triangular matrix efficiently in the memory. This array stores only non-zero elements. To store in a one-dimensional array, we do the mapping between a two-dimensional matrix and a one-dimensional array. We can be done the mapping in any one of the following ways:
(a) Row-wise mapping— Here the contents of array Arr[] will be {1, 2, 2, 1, 4, 3, 9, 8, 7, 1, 1, 2, 7, 8, 9}
(b) Column-wise mapping— Here the contents of array Arr[] will be {1, 2, 1, 9, 1, 2, 4, 8, 2, 3, 7, 7, 1, 8, 9}
2. Upper Triangular Matrix / Sparse Matrix
In the Upper triangular sparse matrix, all elements below the main diagonal have a zero value. This type of sparse matrix is also known as an upper triangular matrix. If you see its pictorial representation, then you find that all the elements having non-zero value are appear above the diagonal.
In an upper-triangular matrix, Arr i,j=0 where i>j. An n*n upper-triangular matrix Arr has n non-zero elements in the first row, n–1 non-zero element in the second row, and likewise one non-zero element in the nth row.
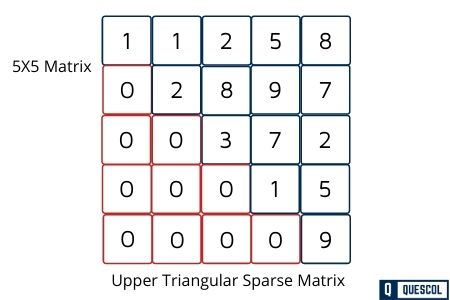
(a) Row-wise mapping— Here the contents of array Arr[] will be {1, 1, 2, 5, 8, 2, 8, 9, 7, 3, 7, 2, 1, 5, 9}
(b) Column-wise mapping— Here the contents of array Arr[] will be {1, 1, 2, 2, 8, 3, 5, 9, 7, 1, 8, 7, 2, 5, 9}
3. Tri-diagonal matrix
Tri-diagonal matrix is also another type of a sparse matrix, where elements with a non-zero value appear only on the diagonal or immediately below or above the diagonal.
In a tridiagonal matrix, Arr i,j=0, where |i – j| > 1.
For matrix being a tridiagonal matrix element should present
(a) On the main diagonal means all non-zero elements at i=j and at all rest place zero. In this case, the total number of non-zero elements is n.
(b) at above the main diagonal means all non-zero elements at i=j–1. In this case, the total number of non-zero elements is n-1.
(c) at below the main diagonal means all non-zero elements for i=j+1. In this case, the total number of non-zero elements is n-1.
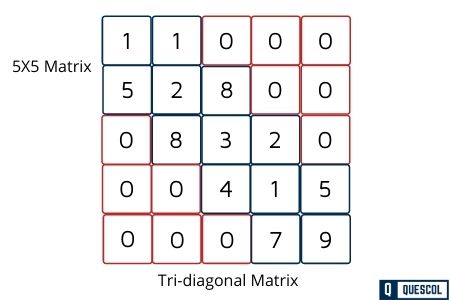
We only store non-zero elements. We can do the mapping between a two-dimensional matrix and a one-dimensional array the following ways:
(a) Row-wise mapping— Here the contents of array Arr[] will be {1, 1, 5, 2, 8, 8, 3, 2, 4, 1, 5, 7, 9}
(b) Column-wise mapping— Here the contents of array Arr[] will be {1, 5, 1, 2, 8, 8, 3, 4, 2, 1, 7, 5, 9}
(c) Diagonal-wise mapping— Here the contents of array Arr[] will be {1, 8, 2, 5, 1, 2, 3, 1, 9, 5, 8, 4, 7}
Why Sparse Matrices Matter
In both types, the zeros play no active role in calculations. This means we can skip them, saving computational resources. When dealing with massive datasets or complex simulations, this efficiency can significantly reduce processing time and memory usage.
Applications of Sparse Matrices
- Scientific Computing: Sparse matrices are used in simulations of real-world phenomena where only a few interactions need to be considered.
- Machine Learning: They help in handling large datasets with missing or insignificant data.
- Network Theory: Sparse matrices represent networks or graphs where connections between nodes are limited.
Storing Sparse Matrices
Storing a sparse matrix efficiently is key. You don’t want to waste space on zeros. Techniques like the Compressed Sparse Row (CSR) or Compressed Sparse Column (CSC) format store only the non-zero elements and their positions, dramatically reducing the storage requirement.
Conclusion
Lower and upper triangular sparse matrices simplify the complexity of mathematical operations by focusing on the non-zero elements. This specificity, combined with efficient storage and processing techniques, makes sparse matrices invaluable in computational mathematics, data science, and beyond. Whether solving linear equations or optimizing machine learning algorithms, understanding and utilizing sparse matrices allows us to tackle larger problems more efficiently, turning vast fields of zeros into focused areas of fruitful computation.
