A graph is an abstract data structure that is basically a collection of a finite set of vertices (also called nodes) and edges that connect these vertices.
A Graph is also known as a non-linear data structure because we can insert data anywhere by following some defined rule anywhere.
Definition
We can define graph G is as an ordered set (V, E), where V(G) represents the set of vertices and E(G) represents the edges that connect these vertices.
In the below figure we have a graph
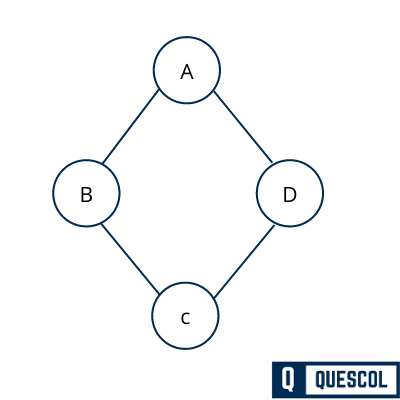
Vertices V(G) = {A, B, C, D}
Edges E(G) = {(A, B), (B, C), (A, D), (C, D)}
Note: All tree can be a graph but all graph cannot be a tree.
There are two types of graph in data structure
Directed Graph
A directed graph G is a graph where each edge of the graph has a direction assigned to it. This direction shows how to go from one vertex to another vertex. A directed graph is also known as a digraph. An edge of a directed graph can be written as an ordered pair (a, b) of nodes in G.
Lets see below example of directed graph
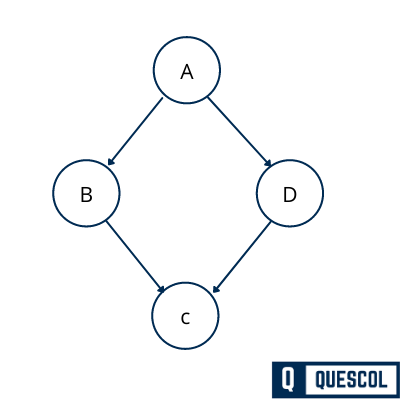
For an edge (A, B),
- The edge starts from vertex A and terminates at vertex B.
- Here a is known as the origin or starting point of edge e and b is known as the destination or terminal point of edge e.
- A is the predecessor of B and B is the successor of A.
- Vertices A and B are adjacent to each other.
Un-Directed Graph
An undirected graph G is a graph where edges of the graph has a no direction assigned to it. It means we can go from one vertex to another vertex in any direction. An edge of a undirected graph can be written as an ordered pair (a, b) of nodes in G.
Lets see below example of undirected graph

For an edge (a, b)
- The edge starts from vertex A and terminates at vertex A.
- Here A is known as the origin or starting point of edge e and B is known as the destination or terminal point of edge e.
- A is the predecessor of B and B is the successor of A.
- Vertices A and B are adjacent to each other.
Some Basic terminology of graph
Adjacent Vertices : Adjacent Vertices of a node ‘a’ is list of all the vertices that are connected by that vertex ‘a’.
Path : It is way to reach one vertix to another vertix. There may be multiple path between two vertix.
Degree: The degree of a node is the sum of in-degree and out-degree of a particular node ‘a’. A degree is written as deg(a).
Therefore, deg(a) = indeg(a) + outdeg(a).
In degree : The in-degree of a node a, is the number of edges that terminate at a. It is written as indeg(a).
Out degree : The out-degree of a node a, is the number of edges that originate at a. It is written as outdeg(a).
