The Tower of Hanoi is a mathematical Puzzle that consists of three towers(pegs) and multiple disks. Initially, all the disks are placed on one rod. And this disks are arranged on one over the other in ascending order of size.
Our Objective is to move all disks from initial tower to another tower without violating the rule.
The Rule For disk movement in TOH
The rules according to which the disks have to be moved in Tower of Hanoi are the following
- Initially, the disks are placed in Increasing Order in size on Tower 1 from top to bottom.
- the objective is to move them to tower 2, making also use of an auxiliary tower 3.
- the conditions for moving the disks are:
- all disks (except the one to be moved) have to be on one of the three towers.
- Only one disk is possible to move at a time.
- The only top disk can be moved i.e. taking from the top of one tower and placing on the top of another tower.
- A larger disk can never be placed on a smaller disk.
History
There is one history behind Tower Of Hanoi is, It is originated from an ancient legend from Vietnam, according to which a group of monks is moving around a tower of 64 disks of different sizes according to certain rules. The legend says that, when the monks will have finished moving around the disks, the end of the world will come.
Tower of Hanoi mathematical puzzle that has n disks with 3 towers can be solved in minimum 2^n−1 steps.
For an example
A puzzle with 3 disks has taken
2^3 – 1 = 7 steps.
Algorithm For Tower of Hanoi Puzzle
In Tower Of Hanoi puzzle we have three towers and some disks. We have to move this disk from intial tower to destination tower using aux tower.
For an example lets take we have two disks and we want to move it from source to destination tower.
So the approach we will follow
- First, we will move the top disk to aux tower.
- Then we will move the next disk (which is the bottom one in this case) to the destination tower.
- And at last, we will move the disk from aux tower to the destination tower.
Similarly if we will have n number of disk then our aim is to move bottom which is disk n from source to destination. And then put all other (n-1) disks onto it.
Steps we will follow is
- Step 1 − Move n-1 disks from source to aux
- Step 2 − Move nth disk from source to dest
- Step 3 − Move n-1 disks from aux to dest
Means to move n > 1 disks from tower 1 to tower 2, using auxiliary tower 3
- Step 1- Move n – 1 disks from Tower 1 to tower 3
- Step 2 – Move the n-th disk from Tower 1 to Tower 2
- Step 3 – Move n – 1 disk from Tower 3 to Tower 2
Pseudo code For Tower of Hanoi Puzzle
START
Procedure TOH(disk, source, dest, aux)
IF disk == 1, THEN
move disk from source to dest
ELSE
TOH(disk - 1, source, aux, dest) // Step 1
moveDisk(source to dest) // Step 2
TOH(disk - 1, aux, dest, source) // Step 3
END IF
END Procedure
STOP
Pictorial Representation of How Tower of Hanoi works
Let's see the below example where we have three disks that have to move in the destination tower which is the middle one with the help of the auxiliary tower.
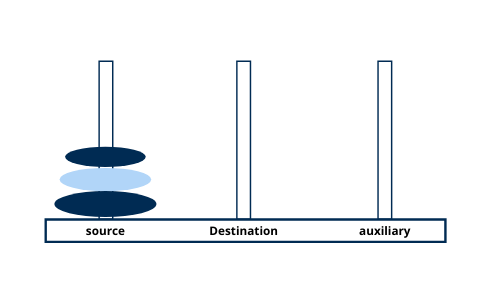
Move disk 1 from tower source to tower destination
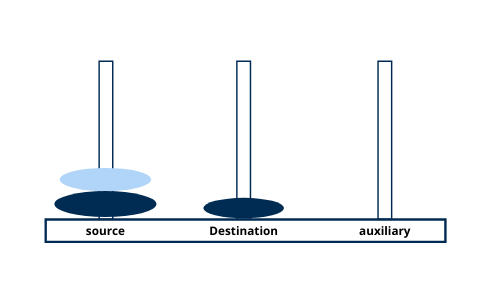
Move disk 2 from tower source to tower auxiliary
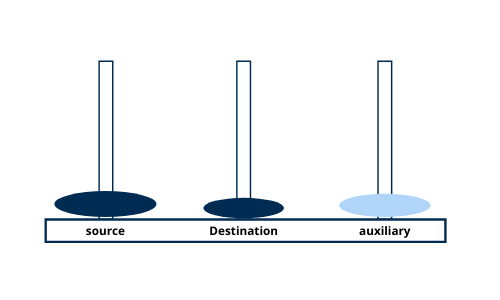
Move disk 1 from tower destination to tower auxiliary
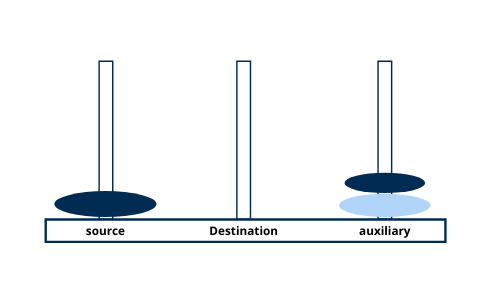
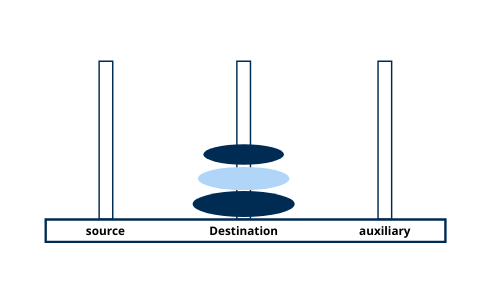
Move disk 3 from tower source to tower destination
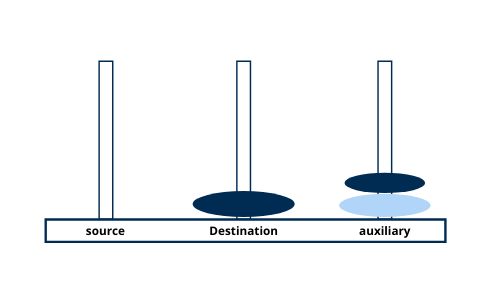
Move disk 1 from tower auxiliary to tower source
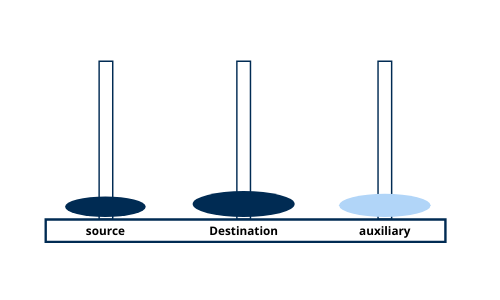
Move disk 2 from tower auxiliary to tower destination
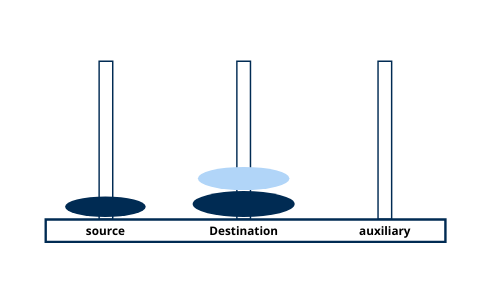
Move disk 1 from tower source to tower destination
C Program to Implement TOH puzzle
#include <stdio.h>
void towerOfHanoi(int n, char source, char dest, char aux) {
if (n == 1) {
printf("Move disk 1 from tower %c to tower %c\n", source, dest);
return;
}
towerOfHanoi(n - 1, source, aux, dest);
printf("Move disk %d from tower %c to tower %c\n", n, source, dest);
towerOfHanoi(n - 1, aux, dest, source);
}
int main() {
int n = 3; // Number of disks
towerOfHanoi(n, 'A', 'B', 'C'); // A, B, and C are names of towers
return 0;
}
Output
Move disk 2 from tower A to tower C
Move disk 1 from tower B to tower C
Move disk 3 from tower A to tower B
Move disk 1 from tower C to tower A
Move disk 2 from tower C to tower B
Move disk 1 from tower A to tower BExplanation
Function: towerOfHanoi
- Parameters: The function takes four parameters:
int n: The number of disks to move.char source: The peg where the disks start.char dest: The peg where the disks need to end up.char aux: An auxiliary peg used for intermediate moves.
- Base Case: If
nis 1 (meaning only one disk is left), it directly moves the disk from thesourcepeg to thedestpeg and prints the action. - Recursive Calls:
- First, it moves
n-1disks from thesourcepeg to theauxpeg, usingdestas an auxiliary peg. This step clears the way to move the largest disk. - Then, it moves the
nth (largest) disk from thesourcepeg to thedestpeg and prints this action. - Finally, it moves the
n-1disks from theauxpeg to thedestpeg, using thesourcepeg as an auxiliary peg, placing them on top of thenth disk.
- First, it moves
Main Function
- Disk Setup: The program defines
n = 3, meaning there are three disks to move. - Solution Call: It calls
towerOfHanoiwithndisks and names the pegs A (source), B (destination), and C (auxiliary) to solve the puzzle. - Execution: The program then executes, displaying each move required to solve the puzzle according to the Tower of Hanoi rules.
Rules Enforced
- Only One Disk at a Time: Each step moves only one disk.
- No Larger Disk on Top of a Smaller Disk: The program’s logic ensures this rule by moving smaller disks out of the way before moving larger ones.
- Use Three Pegs: The solution uses all three pegs effectively to shift the disks from the source to the destination.
Java Program to Implement TOH puzzle
public class TowerOfHanoi
{
static void towerOfHanoi(int n, char source,
char dest, char aux)
{
if (n == 1)
{
System.out.println("Move disk 1 from tower "+
source+" to tower "+dest);
return;
}
towerOfHanoi(n - 1, source, aux, dest);
System.out.println("Move disk "+ n + " from tower " +
source +" to tower " + dest );
towerOfHanoi(n - 1, aux, dest, source);
}
// Driver code
public static void main(String args[])
{
int n = 3; // Number of disks
towerOfHanoi(n, 'A', 'B', 'C'); // A, B and C are name of towers
}
}Output
Move disk 2 from tower A to tower C
Move disk 1 from tower B to tower C
Move disk 3 from tower A to tower B
Move disk 1 from tower C to tower A
Move disk 2 from tower C to tower B
Move disk 1 from tower A to tower BExplanations
The towerOfHanoi Method
- Parameters: It takes four parameters:
int n: The number of disks to move.char source: The starting tower.char dest: The destination tower.char aux: The auxiliary tower used for intermediate moves.
- Base Case: If
nis 1, meaning there’s only one disk left, it directly moves that disk from thesourcetower to thedesttower. This move is printed out. - Recursive Calls:
- The method first moves
n-1disks from thesourcetower to theauxtower, usingdestas an intermediate tower. This step clears the largest disk at the bottom. - Then, it moves the
nth disk (the bottom disk) from thesourcetower to thedesttower. This move is printed out. - Finally, it moves the
n-1disks from theauxtower back to thedesttower, using thesourcetower as an intermediate tower.
- The method first moves
Main Method
- Starting Point: The
mainmethod serves as the entry point of the program. It specifies:int n = 3;: This means there are three disks to move. This value can be changed to increase or decrease the puzzle’s difficulty.towerOfHanoi(n, 'A', 'B', 'C');: It calls thetowerOfHanoimethod with three towers labeled A, B, and C, where A is the source tower, B is the destination tower, and C serves as the auxiliary tower.
Explanation of the Solution
The Tower of Hanoi puzzle solution is a classic example of a recursive algorithm. The idea is to reduce the problem to smaller sub-problems:
- Move
n-1disks to the auxiliary tower. - Move the largest disk to the destination tower.
- Move the
n-1disks from the auxiliary tower to the destination tower.
This recursive strategy is applied until the base case (a single disk) is reached, which is trivial to solve—just move the disk to the destination tower. The beauty of this solution lies in its simplicity and elegance, demonstrating the power of recursion to solve complex problems through a series of simple steps.
