Polynomial representation using linked lists is a critical concept in computer science and mathematics. In this guide, we explore how linked lists can effectively represent polynomials, especially in situations where polynomials are sparse (i.e., have many zero coefficients). Unlike arrays, linked lists provide a dynamic and memory-efficient way of representing polynomials, making operations like addition, subtraction, and multiplication more manageable and efficient. Understanding this representation is crucial for students and professionals dealing with complex mathematical computations and algorithm design.
Understanding Linked Lists
Linked lists are fundamental data structures consisting of a sequence of nodes. Each node typically contains two parts: data and a reference (or pointer) to the next node in the sequence. Unlike arrays, linked lists do not require contiguous memory allocation, making them ideal for dynamic data storage. In the context of polynomial representation, each node in a linked list can represent a term of the polynomial, storing both its coefficient and exponent.
Representing a Polynomial Term
In the linked list representation of a polynomial, each node corresponds to a term of the polynomial. The node structure usually contains three components:
- Coefficient: The numerical multiplier of the term.
- Exponent: The power to which the variable is raised in the term.
- Next: A pointer to the next term (node) in the polynomial.
This structure allows the polynomial to be stored as a linked list, where each node directly represents a term, and the entire list represents the polynomial in its entirety.
Advantages of Using Linked Lists
Using linked lists for polynomial representation offers several advantages:
- Dynamic Size: The size of the polynomial isn’t fixed, allowing for easy addition or removal of terms.
- Efficient Storage: Especially beneficial for sparse polynomials where many coefficients are zero, as it only stores non-zero terms.
- Flexibility: Easier to implement operations like addition, multiplication, and differentiation compared to array-based representations.
Example
To illustrate how a polynomial is represented using a linked list, let’s consider a specific example. Suppose we have a polynomial:
P(x)=7x^3+5x^2−2x+4
This polynomial will be represented as a linked list where each node represents a term of the polynomial.
Node Structure
Each node in the linked list will typically have the following structure:
- Coefficient: The numerical coefficient of the term.
- Exponent: The exponent of the variable in the term.
- Next: A pointer to the next term (node) in the polynomial.
Representation of the Polynomial as a Linked List
- First Node (7x^3):
- Coefficient: 7
- Exponent: 3
- Next: Pointer to the second node
- Second Node (5x^2):
- Coefficient: 5
- Exponent: 2
- Next: Pointer to the third node
- Third Node (-2x):
- Coefficient: -2
- Exponent: 1
- Next: Pointer to the fourth node
- Fourth Node (4):
- Coefficient: 4
- Exponent: 0 (since it’s a constant term)
- Next: NULL (as it is the last term)
Visual Representation
The linked list for polynomial P(x) would visually look like this:
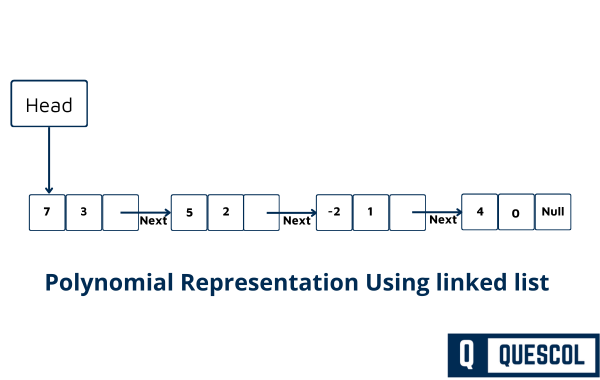
Each box represents a node, with the first number being the coefficient and the second number being the exponent. The arrows indicate the ‘next’ pointers linking each term of the polynomial.
Let’s break down the example of evaluating a polynomial using a linked list for the given polynomial:
P(x)=7x^3+5x^2−2x+4
and calculate its value for x=2.
Step-by-Step Evaluation of Polynomial
- Initial Setup:
- Polynomial: 7x^3+5x^2−2x+4
- Value to evaluate: x=2
- Initialize
Sumto 0.
- Evaluate First Term (7x^3):
- Calculation: 7×2^3
- Process: 7×8=56
- Update Sum=0+56=56
- Evaluate Second Term (5x^2):
- Calculation: 5×2^2
- Process: 5×4=20
- Update Sum=56+20=76
- Evaluate Third Term (-2x):
- Calculation: −2×2
- Process: −2×2=−4
- Update Sum=76−4=72
- Evaluate Fourth Term (4):
- This is a constant term.
- Update Sum=72+4=76
- Conclusion:
- The final value of P(2) is 76.
- So, when we substitute x=2 into the polynomial, the result is 76.
C Program Program to Solve Polynomial
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
struct Node {
int data;
struct Node *next;
struct Node *prev;
};
typedef struct Node Node;
// Create a node
Node* createNode(int coeff, int exp) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->coeff = coeff;
newNode->exp = exp;
newNode->next = NULL;
return newNode;
}
void appendNode(Node** head, int coeff, int exp) {
Node* newNode = createNode(coeff, exp);
if (*head == NULL) {
*head = newNode;
return;
}
Node* temp = *head;
while (temp->next != NULL) {
temp = temp->next;
}
temp->next = newNode;
}
// Function to evaluate the polynomial for a given value of x
int polynomialCalculation(Node* head, int x) {
int sum = 0;
Node* temp = head;
while (temp != NULL) {
sum += temp->coeff * pow(x, temp->exp);
temp = temp->next;
}
return sum;
}
int main() {
Node* poly = NULL;
// Polynomial Construction 7x^3+5x^2−2x+4
appendNode(&poly, 7, 3);
appendNode(&poly, 5, 2);
appendNode(&poly, -2, 1);
appendNode(&poly, 4, 0);
int x = 2;
printf("Polynomial value for x = %d is: %d\n", x, polynomialCalculation(poly, x));
return 0;
}
Output
Polynomial value for x = 2 is: 76
Program Explanations
Header Files (#include Statements):
#include <stdio.h>
#include <stdlib.h>
#include <math.h>stdio.h: Standard input-output header for functions likeprintf.stdlib.h: Standard library header for functions likemalloc.math.h: Math library header for mathematical functions likepow.
Node Structure Definition:
struct Node {
int data;
struct Node *next;
struct Node *prev;
};
typedef struct Node Node;- A
struct Nodeis defined to represent each term of the polynomial. - It contains
coeff(coefficient of the term),exp(exponent of the term), andnext(pointer to the next term).
createNode Function:
// Create a node
Node* createNode(int coeff, int exp) {
Node* newNode = (Node*)malloc(sizeof(Node));
newNode->coeff = coeff;
newNode->exp = exp;
newNode->next = NULL;
return newNode;
}- This function creates a new node with given
coeffandexp. - It allocates memory for a new node, sets its coefficient and exponent, and initializes its
nextpointer toNULL.
appendNode Function:
void appendNode(Node** head, int coeff, int exp) {
Node* newNode = createNode(coeff, exp);
if (*head == NULL) {
*head = newNode;
return;
}
Node* temp = *head;
while (temp->next != NULL) {
temp = temp->next;
}
temp->next = newNode;
}- This function appends a new term/node to the end of the polynomial linked list.
- If the list is empty (
*head == NULL), it sets the head to the new node. - Otherwise, it traverses to the end of the list and appends the new node there.
polynomialCalculation Function:
// Function to evaluate the polynomial for a given value of x
int polynomialCalculation(Node* head, int x) {
int sum = 0;
Node* temp = head;
while (temp != NULL) {
sum += temp->coeff * pow(x, temp->exp);
temp = temp->next;
}
return sum;
}- This function evaluates the polynomial for a given value of
x. - It iterates through each term of the polynomial, calculates its value using
pow(x, exp), multiplies it by the coefficient, and adds it tosum.
main Function:
int main() {
Node* poly = NULL;
// Polynomial Construction 7x^3+5x^2−2x+4
appendNode(&poly, 7, 3);
appendNode(&poly, 5, 2);
appendNode(&poly, -2, 1);
appendNode(&poly, 4, 0);
int x = 2;
printf("Polynomial value for x = %d is: %d\n", x, polynomialCalculation(poly, x));
return 0;
}- The
mainfunction is the entry point of the program. - It first constructs the polynomial
7x^3 + 5x^2 - 2x + 4by appending each term to the linked list. - Then, it evaluates this polynomial for
x = 2using thepolynomialCalculationfunction. - Finally, it prints the calculated value of the polynomial for the given
x.
Hope this article helped you in understanding the writing Program and Algorithm to solve polynomial using linked list.
