Radix Sort: Algorithm, Program, Explanation and Examples

🧑‍💻 By Prakash Kumar • 📝 Updated on: 18 July 2025

Radix sort is a non-comparative sorting algorithm that sorts elements digit by digit starting from least significant digit to most significant digit. It commonly uses Counting Sort or, less frequently, Bucket Sort, as a stable intermediate sorting technique for each digit pass

Suppose if you want to sort 10 elements in ascending order using radix sort, first sort the digit of unit place. After that sort the tenth place digit. This process will go till the most significant digits.

Let’s see an example to understand it clearly

Suppose we have 7 elements in an array.

{101, 45,543,233,321, 833,432}

After sorting unit digit our array will look like

{101, 321,432, 543, 233, 833, 45}

Radix sort uses counting sort as an intermediate sort.

How does radix sort work?

• First Find the largest element in the array. In our case array is {101, 45, 543, 233, 212, 654, 833} and the maximum number in the array is 833 which has 3 digits.
• We find maximum because we have to go up to the most significant digit which is calculated by a total number of digits of the maximum number. The maximum number is 833 and the total number of the digit in 833 is ‘3’. so the loop will go up to a hundred places.
• Visit each significant place one by one from least significant digits to most significant digits. Here we sort elements of each signification digits using counting sort which is non-comparison sorting.

Let’s see a step-wise procedure how to sort elements using radix sort.

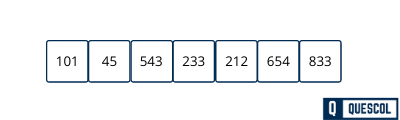
With the help of algorithm we will sort the unit digit of the input array i.e. least significant digit

So after first pass array will become

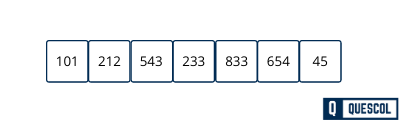
Now we will sort the tenth digit place of the input array

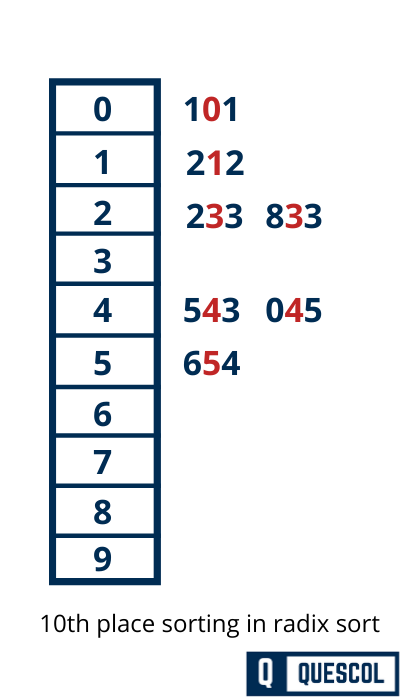
So after the second pass array will look like

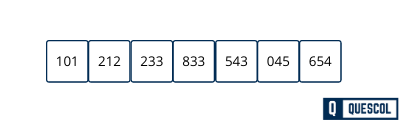
Now we will sort the 100th digit place of the input array i.e. most significant place

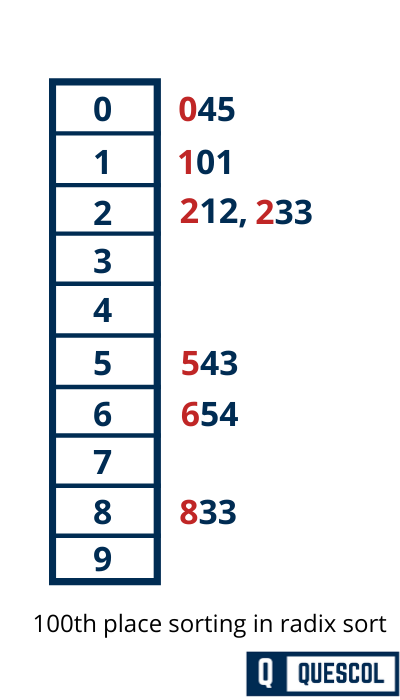
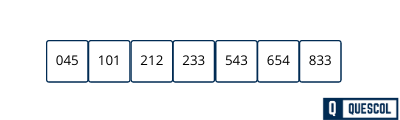
After the third pass array will be sorted

Radix Sort Algorithm

Step 1: Find the maximum number in ARR as Max
Step 2: Calculate the Number of digits in Max and SET NOS = number of digit
Step 3: Repeat Step 4 to 8 for PASS = 1; PASS <= NOS
Step 4: Repeat Step 5 to 7for I=0 to I < Size of ARR
Step 5: SET DIGIT = Arr[I]
Step 6: Insert element Arr[I] to the bucket at index DIGIT
Step 7: Do Increment in bucket count for index DIGIT
[END OF FOR Loop]
Step 8: Pick elements from the bucket starting from index 0 and put in ARR
[END OF For LOOP]
Step 9: END

Radix Sort Algorithm (Pseudocode)

def radixSort(arr):
    max_val = max(arr)
    exp = 1
    while max_val // exp > 0:
        countingSort(arr, exp)
        exp *= 10

Radix Sort Complexity

Scenario	Time Complexity	Explanation
Best Case	O(d × n)	All elements have similar lengths; stable sort (like Counting Sort) is efficient
Average Case	O(d × n)	d = number of digits; n = number of elements
Worst Case	O(d × n)	Even in worst case, Radix Sort is faster than comparison-based sorts
Space Complexity	O(n + b)	b = base (e.g., 10); extra space used by Counting Sort
Stable Sort	Yes	Maintains relative order of equal elements
In-Place Sort	No	Uses extra space for buckets or counting arrays
Comparison-Based	No	Uses digit-based sorting, not element-to-element comparison

Where:

• n = number of elements
• d = number of digits in the largest number
• b = base of number system (commonly 10 for decimal)

Radix Sort Program in C

#include <stdio.h>
int getMax(int arr[], int n) {
    int max = arr[0];
    for (int i = 1; i < n; i++)
        if (arr[i] > max)
            max = arr[i];
    return max;
}

void countSort(int arr[], int n, int exp) {
    int output[n];
    int i, count[10] = {0};
    for (i = 0; i < n; i++)
        count[(arr[i] / exp) % 10]++;
    for (i = 1; i < 10; i++)
        count[i] += count[i - 1];
    for (i = n - 1; i >= 0; i--) {
        output[count[(arr[i] / exp) % 10] - 1] = arr[i];
        count[(arr[i] / exp) % 10]--;
    }
    for (i = 0; i < n; i++)
        arr[i] = output[i];
}

void radixSort(int arr[], int n) {
    int m = getMax(arr, n);
    for (int exp = 1; m / exp > 0; exp *= 10)
        countSort(arr, n, exp);
}

int main() {
    int arr[100],i,n;
    printf("Enter the number of elements you want to sort:\n");
    scanf("%d",&n);
    printf("Now enter the %d elements you want to sort: \n",n);
    for(i=0;i<n;i++){
        scanf("%d",&arr[i]);
    }
    printf("before sorting:\n");
    for(i=0;i<n;i++){
        printf("%d \t",arr[i]);
    }
    radixSort(arr, n);
    printf("\nSorted array: \n");
    for (int i = 0; i < n; i++)
        printf("%d \t", arr[i]);
    printf("\n"); 
    return 0;
}

Output :

Enter the number of elements you want to sort:
5
Now enter the 5 elements you want to sort: 
23
11
43
56
12
before sorting:
23      11      43      56      12 
Sorted array: 
11      12      23      43      56 

Step-by-Step Execution of Radix Sort

We’ll sort based on digits, starting from the least significant digit (LSD) to the most significant digit (MSD) using Counting Sort.

Step 1: Find Maximum Element

We find the maximum number in the array to determine how many digit places we need to process.

• Maximum = 56
• Max has 2 digits ⇒ we need to do 2 passes: for unit place (exp=1) and tens place (exp=10)

Pass 1: exp = 1 (Sort by unit place)

Let’s extract unit digits of each number:

Number	Unit Digit (num / 1 % 10)
23	3
11	1
43	3
56	6
12	2

Now sort the numbers based on these unit digits using stable Counting Sort.

Counting Sort (by unit digit):

1). Count frequencies:

Digit: 0 1 2 3 4 5 6 7 8 9
Count: 0 1 1 2 0 0 1 0 0 0

2). Compute cumulative count:

Digit: 0 1 2 3 4 5 6 7 8 9
Cumulative: 0 1 2 4 4 4 5 5 5 5

3). Build output array (from right to left for stability):

12 (unit=2): count[2] = 2 → place at index 1 → decrement count[2]

56 (unit=6): count[6] = 5 → place at index 4 → decrement count[6]

43 (unit=3): count[3] = 4 → place at index 3 → decrement count[3]

11 (unit=1): count[1] = 1 → place at index 0 → decrement count[1]

23 (unit=3): count[3] = 3 → place at index 2 → decrement count[3]

Output array after Pass 1 (sorted by units digit):

[11, 12, 23, 43, 56]

Pass 2: exp = 10 (Sort by tens place)

Now extract tens digit:

Number	Tens Digit (num / 10 % 10)
11	1
12	1
23	2
43	4
56	5

Counting Sort (by tens digit):

1). Count frequencies:

Digit: 0 1 2 3 4 5 6 7 8 9
Count: 0 2 1 0 1 1 0 0 0 0

2). Cumulative count:

Digit: 0 1 2 3 4 5 6 7 8 9
Cumulative: 0 2 3 3 4 5 5 5 5 5

3). Build output array (from right to left for stability):

56 (tens=5) → count[5]=5 → place at index 4

43 (tens=4) → count[4]=4 → index 3

23 (tens=2) → count[2]=3 → index 2

12 (tens=1) → count[1]=2 → index 1

11 (tens=1) → count[1]=1 → index 0

Output array after Pass 2 (sorted by tens digit):

[11, 12, 23, 43, 56]

Summary Table of Passes

Pass	Digit Place	Array after Pass
Pass 1	Units (exp = 1)	[11, 12, 23, 43, 56]
Pass 2	Tens (exp = 10)	[11, 12, 23, 43, 56]

Real time Application of Radix sort

Radix Sort, known for its efficiency with large sets of data, finds practical applications in areas where the sorting of numerically represented data is crucial. A notable real-time application of Radix Sort is in the sorting of large databases, such as customer records, where each record is assigned a unique numerical identifier or key.

Database Sorting

In database management, especially those handling extensive sets of numeric IDs, Radix Sort can efficiently organize records by sorting them based on these identifiers. This sorting facilitates faster retrieval, search, and organization of data, essential for maintaining high-performance databases.

Sorting Phone Numbers

Telecommunication companies often deal with vast databases of phone numbers. Radix Sort can quickly sort these numbers, helping in efficient management, quick search, and retrieval operations, and ensuring customer data is organized systematically.

Sorting Dates

Applications that involve sorting dates, such as scheduling software, event management systems, and archival records, benefit from Radix Sort. By treating dates as numeric values (e.g., YYYYMMDD), Radix Sort can efficiently organize them in chronological order.

IP Address Sorting

In network management, sorting IP addresses is crucial for various tasks, including routing, allocation, and security. Radix Sort, with its ability to handle numbers efficiently, can sort IP addresses faster than comparison-based algorithms, improving network management operations.

❓FAQs on Radix Sort

Q1. What is Radix Sort?

Answer: Radix Sort is a non-comparative integer sorting algorithm that sorts numbers by processing individual digits. It works by sorting numbers digit by digit starting from the least significant digit (LSD) to the most significant digit (MSD), using a stable sort like Counting Sort.

Q2. Is Radix Sort stable?

Answer: Yes, Radix Sort is stable, meaning it preserves the relative order of elements with equal values. This is possible because it uses a stable intermediate sort like Counting Sort.

Q3. Can Radix Sort be used to sort negative numbers?

Answer: The basic Radix Sort algorithm works only for non-negative integers.
To handle negative numbers, you must:

• Separate negative and positive numbers
• Sort each group individually
• Reverse the sorted negatives and merge with sorted positives

Q4. What is the time complexity of Radix Sort?

Answer: Best/Average/Worst Case: O(d × n)
where d is the number of digits in the maximum number and n is the number of elements.
If the numbers have fixed digit lengths, it behaves like O(n) linear time.

Q5. What is the space complexity of Radix Sort?

Answer: The space complexity is O(n + b), where:

• n = number of elements
• b = base (commonly 10 for decimal numbers)

Q6. Is Radix Sort faster than Quick Sort or Merge Sort?

Answer: It can be faster in specific cases:

• When sorting integers or fixed-length strings
• When the number of digits is significantly smaller than n log n
  However, it’s not comparison-based, so it’s unsuitable for generic data types or floating-point numbers.

Q7. Why is Counting Sort used in Radix Sort?

Answer: Counting Sort is used because it is:

• Stable
• Has linear time complexity O(n + k)
  This makes it perfect for sorting digits (0–9) efficiently without breaking the order of similar digits.

Q8. Can Radix Sort be used for strings?

Answer: Yes! Radix Sort can sort strings of fixed length, such as words of the same number of characters. It sorts from the rightmost character to the leftmost using a stable sort.

Q9. Is Radix Sort an in-place sorting algorithm?

Answer: No. Radix Sort is not in-place because it requires extra space for intermediate arrays (like the output[] array in Counting Sort).