An AVL tree is a self-balancing binary search tree. It was named AVL on its inventor Adelson-Velsky and Landis. There are some scenarios in the Binary search tree where complexity can go O(n) in the worst-case search. so to get search in O(log n) in worst case AVL tree is designed.
Property of AVL tree is the difference of the height of its left and right subtree can be either -1, 0, and 1, this is also known as balance factor. If the balance factor is other than these three values then rebalancing required to maintain this property.
Balance Factor = height(left subtree)-height(right subtree)
Lets see the below example to understand this property
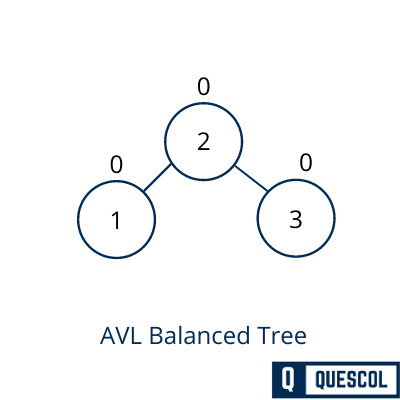
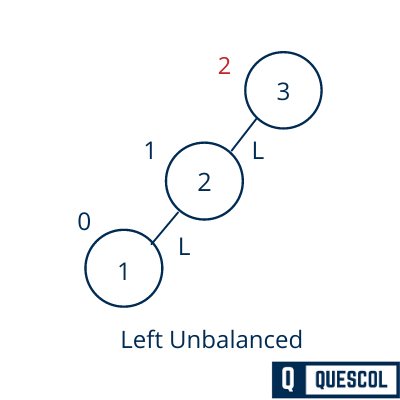
To persist its property and deal with the unbalanced trees there is some rotation that we can apply on the AVL tree.
There are 4 types of rotation to maintain AVL tree property
- LR (left right) rotation
- RR (right right) rotation
- LR(Left Right) rotation
- RL(Right Left) rotation
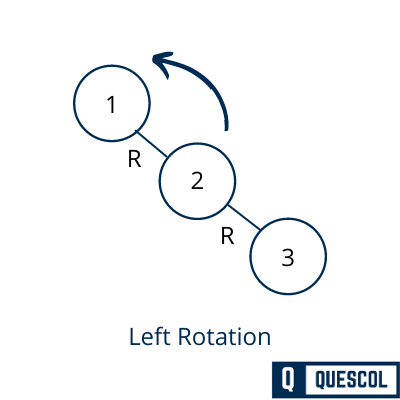
1). Left Rotation
If a tree becomes unbalanced, means the balance factor of a node becomes 2. This has happened when a node is inserted into the right subtree of the right subtree. So to maintain the AVL tree property we do left rotation shown below in figure
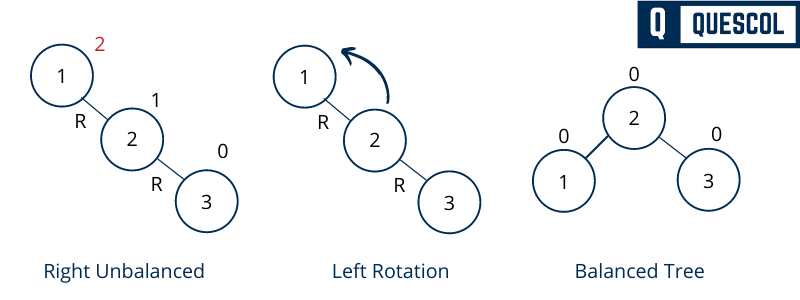
In the above example, node 1 has become unbalanced because its balanced factor becomes 2. Here We perform the left rotation by making 2 the root and 1 as left node of 2.
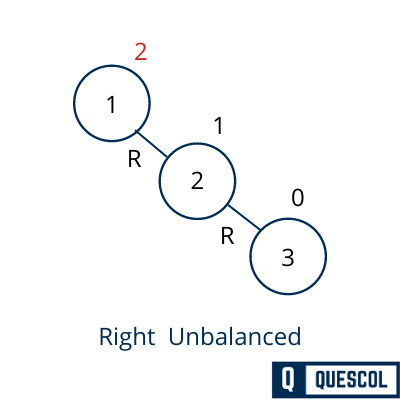
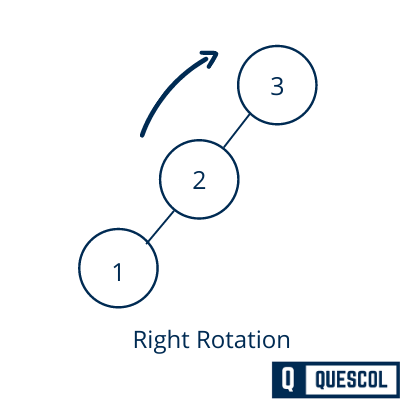
2). Right Rotation
If a tree becomes unbalanced, means the balance factor of a node becomes 2. This has happened when a node is inserted into the left subtree of the Left subtree. So to maintain the AVL tree property we do right rotation shown below in figure
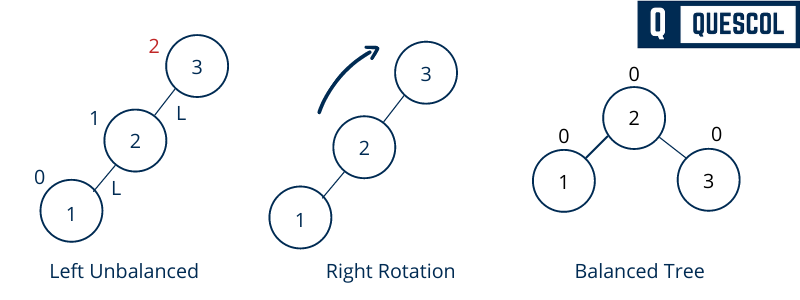
In the above example, node 3 has become unbalanced because its balanced factor is 2. Here We perform the right rotation by making 2 the root and 3 as the right node of 2.
3). Left-Right Rotation
In this case, a node has inserted into the right subtree of the left subtree. So node 3 becomes an unbalanced node because its balance factor is 2 (2-0). So to balance it we perform left-right rotation means first left rotation and then right rotation.
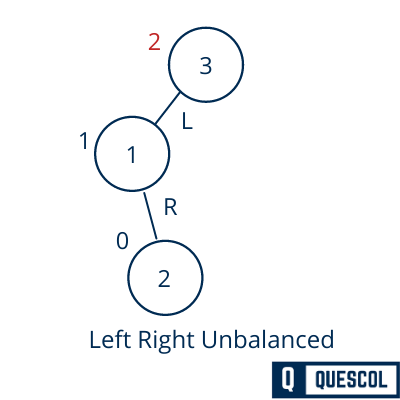
We first perform the left rotation on the left subtree of 3. This rotation will make 1 left subtree of 2.
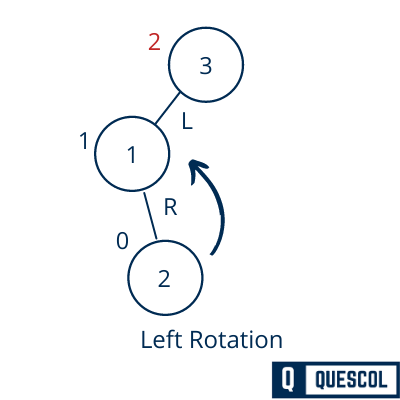
Now after the left rotation tree will be still unbalanced because the Balance Factor of 3 becomes 2. it is because of the left subtree of the left-subtree.
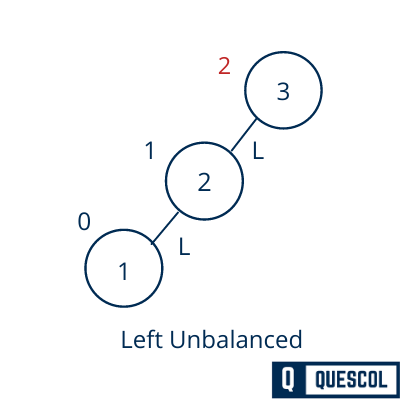
We will now perform the right rotation to balance node 3.
The tree is now balanced.

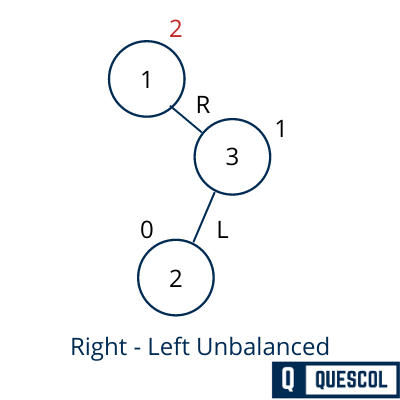
4). Right-Left Rotation
In this case, a node has inserted into the left subtree of the right subtree. So node 3 becomes an unbalanced node because its balance factor is 2 (2-0). So to balance it we perform left-right rotation means first left rotation and then right rotation.
We first perform the right rotation on the right subtree of 1. This rotation will make 3 right subtree of 2.
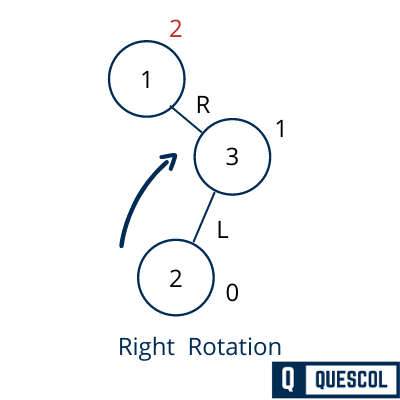
Now after the right rotation tree will be still unbalanced because the Balance Factor of 1 becomes 2. it is because of the right subtree of the right-subtree.

We will now perform the right rotation to balance node 1
The tree is now balanced.

Advantages of AVL Trees
- Fast Searches: Because it’s balanced, finding something in an AVL Tree is like finding a book in a well-organized shelf. You know exactly where to look.
- Efficient Updates: Adding or removing items doesn’t make a mess. The tree quickly tidies up, staying balanced.
- Reliable Performance: With balance, the tree promises that no task will take too long, making it dependable.
Real-World Example
Imagine you’re using a contact app to store your friends’ numbers. Behind the scenes, the app uses an AVL Tree to keep the numbers. When you add a new friend, the app places that number in the tree. If the tree becomes unbalanced, it uses its rotation moves to balance itself. This way, when you search for a friend’s number, the app can find it super fast, thanks to the balanced tree.
Conclusion
An AVL Tree is like a magical bookshelf that keeps itself organized no matter how many books you add or take away. It ensures that everything is always balanced, making it easy and fast to find any book (or piece of data) you need. This special tree is a powerful tool in the world of programming, helping computers and apps run efficiently and reliably.
