Implement Stack using Singly linked list

Stack can be implemented by both array and linked list.

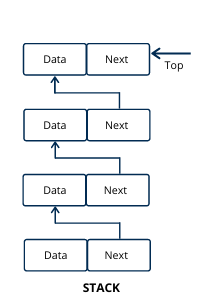
There is some limitation or you can say that drawback in stack implementation using an array is that the array must be declared with some fixed size. In case if the size of the array becomes small to perform the required operation so this is a problem or if we declare the too larger size of an array in advance then it is also a wastage of memory. So if the array size cannot be determined in advance, then we have an alternative solution that is linked list representation.
The storage requirement of linked representation of the stack with n elements is O(n), and the typical time required for the operations is O(1).
In a linked stack, every node has two parts—one that stores data and another that stores the address of the next node. The linked list allocates the memory dynamically. However, time complexity in both the scenario is the same for all the operations i.e. push, pop, and peek. The START pointer of the linked list is used as TOP. All insertions and deletions are done at the node pointed by TOP. If TOP = NULL, then it indicates that the stack is empty.

OPERATIONS ON A LINKED STACK

A linked stack supports all the three stack operations, that is, push, pop, and peek.

1). Push Operation

The push operation is used to insert an element into the stack. The new element is added at the topmost position of the stack.

Push Operation algorithm

Step 1 – Allocate memory to create a newNode with given value and name it as NEW_NODE.
Step 2 – Check whether TOP == NULL of Stack
Step 3 – If TOP == NULL means empty, then set newNode → next = NULL and TOP = NEW_NODE.
Step 4 – If TOP != NULL, then set newNode → next = top and TOP = NEW_NODE.
Step 5 – END

2). POP Operation

POP operation is performed on stack to remove item from the stack.

POP Operation algorithm

Step 1 – Check whether TOP == NULL of Stack.
Step 2 – If TOP == NULL then print “Stack is Empty” and terminate the function
Step 3 – If TOP != NULL, then define a Node pointer ‘temp’ and set it to ‘top’.
Step 4 – Then set ‘top = top → next’.
Step 5 – Finally, delete ‘temp’. (free(temp)).

3). PEEK Operation

Using peek operation topmost element of the stack will be retrieved without deleting it from the stack. 

PEEK Operation Algorithm

Step 1 – Check whether TOP == NULL of Stack.
Step 2 – If TOP == NULL then print “Stack is Empty” and terminate the function
Step 3 – If TOP != NULL, then display top->data.
Step 4 – END

4). Display Operation

Display operation is used to print all the elements of stack.

Display Operation Algorithm

Step 1 – Check whether TOP == NULL of Stack.
Step 2 – If TOP == NULL then print “Stack is Empty” and terminate the function
Step 3 – If TOP != NULL, then define a Node pointer ‘ptr’ and initialize with top.
Step 4 – Display ‘temp → data’ util temp → next != NULL.
Step 5 – Finally Display ‘temp → data’.

Java Program for Stack implementation using linked list

public class Main {
    static class StackNode {
        int data;
        StackNode next;
        StackNode(int data) { 
            this.data = data; 
        }
    }
    
    StackNode root;
    
    public void push(int data) {
        StackNode newNode = new StackNode(data);
        if (root == null) {
            root = newNode;
        } else {
            StackNode temp = root;
            root = newNode;
            newNode.next = temp;
        }
        System.out.println("Item pushed into stack = " + data);
    }

    public int pop() {
        int popped;
        if (root == null) {
            System.out.println("Stack is Empty");
            return 0;
        } else {
            popped = root.data;
            root = root.next;
            return popped;
        }
    }

    public int peek() {
        if (root == null) {
            System.out.println("Stack is empty");
            return Integer.MIN_VALUE;
        } else {
            return root.data;
        }
    }

    public static void main(String[] args) {
        Main m = new Main();
        m.push(10);
        m.push(20);
        m.push(30);
        System.out.println("Item popped from stack = " + m.pop());
        System.out.println(m.peek() + " Returned by Peek operation");
    }
}

Output

Item pushed into stack = 10
Item pushed into stack = 20
Item pushed into stack = 30
Item popped from stack = 30
20 Returned by Peek operation