In hashing technique, Collison is a situation when hash value of two key become similar.
Suppose we want to add a new Record with key k in a hashtable, but index address H(k) is already occupied by another record. This situation is known as a collision.
Example to understand the Collision Situation
In the below figure, we have a hash table and the size of the below hash table is 10.
It means this hash table has 10 indexes which are denoted by {0, 1,2,3,4,5,6,7,8,9}
Now we have to insert value {9,7,17,13,12,8} into a hashtable. So to calculate slot/index value to store items we will use hashing concept.
And hash function is h(k) = h(k) mod m
Step 1:
First Draw an empty hash table of Size 10.
The possible range of hash values will be [0, 9].

Step 2:
Insert the given keys one by one in the hash table.
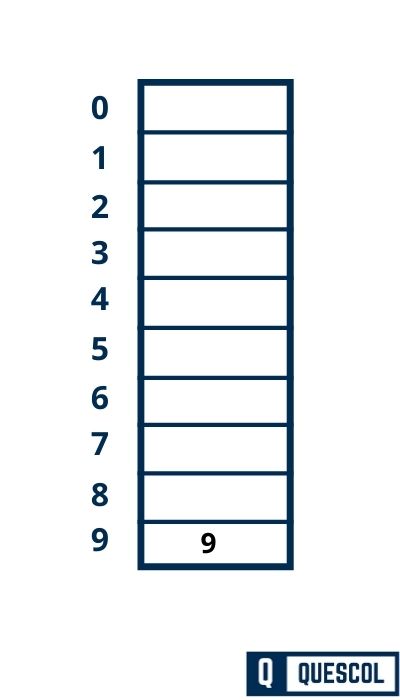
First Key to be inserted in the hash table = 9.
h(k) = h(k) mod m
h(9) = 9 mod 10 = 9
So, key 9 will be inserted at index 9 of the hash table
Step 3:
Insert the given keys one by one in the hash table.
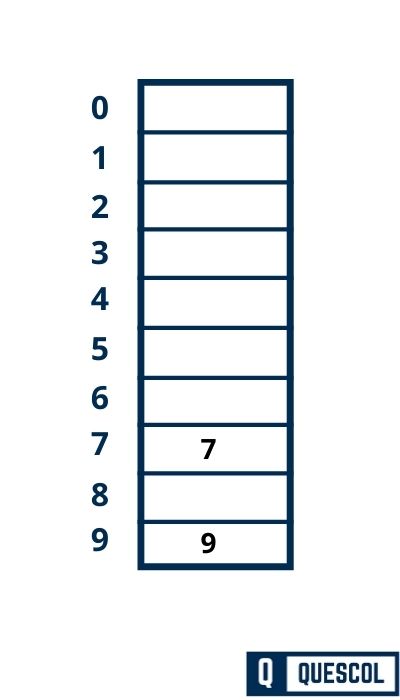
Second Key to be inserted in the hash table = 7.
h(k) = h(k) mod m
h(7) = 7 mod 10 = 7
So, key 7 will be inserted at index 7 of the hash table
Step 4:
Insert the given keys one by one in the hash table.
Second Key to be inserted in the hash table = 17.
h(k) = h(k) mod m
h(7) = 17 mod 10 = 7
So, key 17 will be inserted at index 7 of the hash table
But Here at index 7 already there is a key 7. So this is a situation when we can say a collision has occurred.
Now to overcome this situation we have various Collision resolution techniques.
Collision Resolution Techniques
1). Open Addressing
a. Linear Probing
b. Quadratic Probing
c. Double Hashing Technique
2). Closed Addressing
a. Chaining
1). Open Addressing
In open addressing, all the keys are stored inside the hash table and
No key is stored outside the hash table.
a). Linear Probing
- The simplest approach to resolve a collision is linear probing. In this technique, if a value is already stored at a location generated by h(k), it means collision occurred then we do a sequential search to find the empty location.
- Here the idea is to place a value in the next available position. Because in this approach searches are performed sequentially so it’s known as linear probing.
- Here array or hash table is considered circular because when the last slot reached an empty location not found then the search proceeds to the first location of the array.
Clustering is a major drawback of linear probing.
Below is a hash function that calculates the next location. If the location is empty then store value otherwise find the next location.
Following hash function is used to resolve the collision in:
h(k, i) = [h(k) + i] mod m
Where
m = size of the hash table,
h(k) = (k mod m),
i = the probe number that varies from 0 to m–1.
Therefore, for a given key k, the first location is generated by [h(k) + 0] mod m, the first time i=0.
If the location is free, the value is stored at this location. If value successfully stores then probe count is 1 means location is founded on the first go.
If location is not free then second probe generates the address of the location given by
[h(k) + 1]mod m
Similarly, if the generated location is occupied, then subsequent probes generate the address as
[h(k) + 2]mod m, [h(k) + 3]mod m, [h(k) + 4]mod m, [h(k) + 5]mod m
, and so on, until a free location is found.
Probes is a count to find the free location for each value to store in the hash table.
b). Quadratic Probing
In this technique, if a value is already stored at a location generated by h(k), then the following hash function is used to resolve the collision:
h(k, i) = (h(k) + i^2) mod m
where m is the size of the hash table,
h(k) = (k mod m), i is the probe number that varies from 0 to m–1,
- Quadratic probing solves the clustering problem which is in linear probing because instead of doing a linear search, it does a quadratic search.
- For a given key k, first, the location generated by [h(k) + 0] mod m, where i is 0. If the location is free, the value is stored at this generated location, else new locations will be generated using hash function [h(k) + 1^2] mod m.
- Value of i will change until free space is founded and probe count is increased until free space is founded.
Quadratic probing performs better than linear probing, in order to maximize the utilization of the hash table. - The disadvantage of quadratic probing is it does not search all locations of the list.
c). Double Hashing
- Double hashing is a collision resolution technique used in conjunction with open-addressing in hash tables.
- In this technique, we use a two hash function to calculate empty slot to store value.
- In the case of collision we take the second hash function h2(k) and look for i * h2(k) free slot in an ith iteration.
- Double hashing requires more computational time becuase two hash functions need to be computed.
To start with, double hashing uses two hash function to calculate an empty location.
In double hashing, we use two hash functions rather than a single
function. The hash function in the case of double hashing can be given as:
h(k, i) = [h1(k) + ih2(k)] mod m
where m is the size of the hash table,
h1(k) and h2(k) are two hash functions
h1(k) = k mod m,
h2(k) = k mod m
i is the probe number that varies from 0 to m–1
When we have to insert a key k in the hash table, we first probe the location given by applying
[h1(k) mod m] because during the first probe, i = 0. If the location is vacant, the key is inserted into it.
And if the location is not vacant then increase value of i to calculate next location using
h(k,1) = [h1(k) + 1*h2(k)] mod m
Otherwise
h(k,0) = [h1(k) + 0*h2(k)] mod m
for the next key.
2). Closed Addressing
In closed addressing, all the keys are stored inside and outside the hash table. Each slot of the hashtable is linked with linked list So if a collision occurs key stores in the linked list.
a). Chaining
- Chaining is a Collision Resolution technique in hash tables.
- In hash tables collision occurs when two keys are hashed to the same index in a hash table.
- It means the calculated hash value for the two keys is the same. Collisions are a problem because every slot in a hash table is supposed to store a single element.
- In the chaining approach, the hash table is an array of linked lists. This means each index of the hash table has its own linked list.
- And if Collision arises then a new value will be store in the linked list of that index. And at index, this linked list appears like a chain that is why this technique is known as the chaining technique.
Time complexity of Chaining
For Searching
In worst case all the value is present in the linked list of the same index. So in this case sequential search is performed to search the value.
So in the worst case, time complexity will be O(n) for searching.
Conclusion
Collision resolution techniques are crucial in hashing. They ensure that every piece of data has its place, making data retrieval fast and efficient. Whether through chaining, open addressing, or double hashing, these methods keep our data organized and accessible, much like a well-run library or a school with enough lockers for everyone. Understanding and applying these techniques allows for the efficient handling of data, making our digital world run smoothly.
