Binary Search Algorithm in Data Structure with Explanation

by

Binary search is a very efficient searching technique for finding an element from a sorted Array. This technique follows the divide and conquers approach to perform a searching operation.

Suppose we have 10,000 sorted elements in an array and want to search a value in that array. If we follow linear searching, then in the worst case, we have to compare search value with all 10,000 elements in the list.

But when we use binary search, we need only log n base two comparison means 14 comparisons only in the worst case. So you can see how binary search is efficient for more massive data in comparison to the linear searching technique.

Binary search is also known as a half-interval search and logarithmic search in computer science.

In this technique, we first find the middle element from the sorted array, and then we break it into two half parts and then compare the search value with the middle element.

  • If the search value is equal to the middle value, then return the middle-value index means search value found in the middle.
  • If the search value is greater than the middle value, then the next search will only be done on the second half array.
  • If the search value is smaller than the middle value, then the next search will be done in the first half of the array.
  • And if the search value is not found anywhere, it will return -1 or any message like “no item found”.

How Binary Search Works

  1. Start in the Middle: Find the middle item of the sorted list.
  2. Compare: Check if the middle item is the one you’re looking for. If it is, you’re done!
  3. Decide Which Half to Keep: If the item you want is greater than the middle item, ignore the first half of the list. If it’s less, ignore the second half.
  4. Repeat: Choose the new middle of the list you kept and repeat the process until you find the item or until there’s nowhere left to search.

Binary Search Algorithm

Step 1. Start with a sorted array
Step 2. Find the middle element and divide it into two-part.
Step 3. Compare the search value with the middle element if match found, then return the middle index. If not, then follow step 4 and step 5 accordingly.
Step 4. If the search value is greater than the middle, then select the right part of the array after division and follow step 2
Step 5. If the search value is lesser than the middle, then select the left part of the array after division and follow step 2
Step 6. When a match is found, then return the index of the element.
Step 7. If no match is found, then return -1.

function binary_search(K, n, X) is
    L = 0
    R = n − 1
    while L ≤ R do
        m = round((L + R) / 2)
        if K[m] < X then
            L = m + 1
        else if K[m] > X then
            R = m − 1
        else:
            return m
    return -1

Binary search time complexity

Worst-case performance O(log n)
Best-case performance O(1)
Average performance O(log n)
Worst-case space complexity O(1)

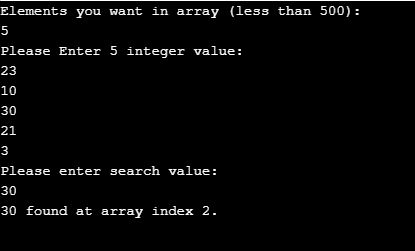
Simple Binary Search Program in C

#include <stdio.h>
int main()
{
  int first, last, middle, n, i, value, arr[500];

  printf("Elements you want in array (less than 500): \n");
  scanf("%d", &n);

  printf("Please Enter %d integer value:\n", n);

  for (i = 0; i < n; i++)
    scanf("%d", &arr[i]);

  printf("Please enter search value: \n");
  scanf("%d", &value);

  first = 0;
  last = n - 1;
  middle = (first+last)/2;

  while (first <= last) {
    if (arr[middle] < value){
      first = middle + 1;
    }
    else if (arr[middle] == value) {
      printf("%d found at array index %d.\n", value, middle);
      break;
    }
    else{
      last = middle - 1;  
    }
    middle = (first + last)/2;
  }
  if (first > last){
    printf("%d isn't present in the list.\n", value);
  }
  return 0;
}

Output:

Binary Search Algorithm
  • Sorted List: It only works if the list is sorted because that’s how it knows which half of the list to keep.
  • Efficiency: It’s very fast, especially compared to looking at every item one by one. Imagine searching for one page in a book of 1000 pages; binary search finds it in just 10 steps or less.
  • Implementation: It can be done iteratively, using loops, or recursively, where the function calls itself with a smaller portion of the list each time.
  • Finding a Word in a Dictionary: Just like searching for a word in a dictionary by starting in the middle, then deciding which half of the dictionary to continue searching in.
  • Looking Up a Contact in a Phone: When you search for a contact in your phone, your phone uses binary search to find the name quickly if your contacts are sorted alphabetically.
  • Speed: It finds items quickly, even in very large lists, by cutting the search area in half each time.
  • Simplicity: The concept is straightforward, making it easy to understand and implement.
  • Efficiency: Uses fewer steps to find an item, saving time and resources.
  • In Computer Science: Used in searching algorithms, databases, and handling large datasets where quick search operations are crucial.
  • In Everyday Life: Whenever choices are made by halving options – like finding a player’s rank in a sorted leaderboard.

Conclusion

Binary Search is like a treasure hunt where you cleverly eliminate half of the places where the treasure isn’t hidden each time, dramatically speeding up the discovery process. It exemplifies efficiency and simplicity, proving that a methodical approach often leads to the quickest solutions. Whether through games, searching for contacts, or even deciding between choices, the principles of Binary Search find their way into our daily decision-making, showcasing the power and elegance of this algorithm.