A B-tree is an extended version of m-way. There are some drawbacks with the m way tree is, in the worst case, it may behave like a linked list because it has no rule over the number of keys in node. To resolve this B-tree is introduced which is balanced. Here balanced means all leaf nodes should be at the same level which is not in the m-way tree and also each node can have some minimum and a maximum number of keys.
Here, Key in node = Order of B tree – 1
B-tree of Order m has the following
Property
- All leaf node must be at the same level,
- All nodes except root must have at least m/2 – 1 key and a maximum of m-1 one key.
- Each node of B-Tree has a maximum of m children and a minimum of m/2 children.
- All the key values in a node must be in ascending order.
- B Tree grows bottom to top.
Properties of B-trees
- Balanced: Every path from the root (the top of the tree) to the leaves (the bottom) is the same length. This keeps the tree balanced, like a seesaw that’s perfectly level.
- Multiple Keys in a Node: Unlike other trees, where each spot can hold only one key, B-tree nodes can hold many keys, making them more efficient.
- Sorted Order: Keys in B-trees are always sorted, making it easy to search for information.
- Variable Node Sizes: The nodes can adjust, becoming bigger or smaller as needed, which helps keep the tree balanced.
B-Tree was developed in the year 1972 by Bayer and McCreight. At first its name was Height Balanced m-way Search Tree but later it was changed as B-Tree.
Because of the balance property of B-Tree it allows searches, insertions, and deletions in logarithmic time.
And More benefits of its over self-balancing binary search trees(AVL Tree), It can store multiple keys at each node.
B-Tree is mostly used to optimized systems that read and write because every node contains more keys so that we can transfer large blocks of data at on reading or write operation. And Also searching in log n times. It is mostly used in database and file systems to perform read and write operations.
Time Complexity of B-Tree
| S. No. | ALGORITHM | TIME COMPLEXITY |
| 1 | Search | O(log n) |
| 2 | Insert | O(log n) |
| 3 | Delete | O(log n) |
“n” is the total number of elements in the B-tree.
Insertion Operation in B-trees
Adding new information to a B-tree is like adding a new book to our magical bookshelf.
Here’s how it works:
- Find the Right Spot: First, we find where the new book (or piece of information) should go, keeping everything in sorted order.
- Add If There’s Space: If there’s room on the shelf (node), we just put the book there.
- Split if Needed: If the shelf is full, we split it into two. We take the middle book and move it up a level (or create a new level if necessary). This split keeps the tree balanced and makes sure there’s room for everything.
- Repeat as Necessary: If moving a book up causes the shelf it moves to become too full, we split that shelf too, and so on, until everything is neatly organized again.
Example of Insertion in B Tree
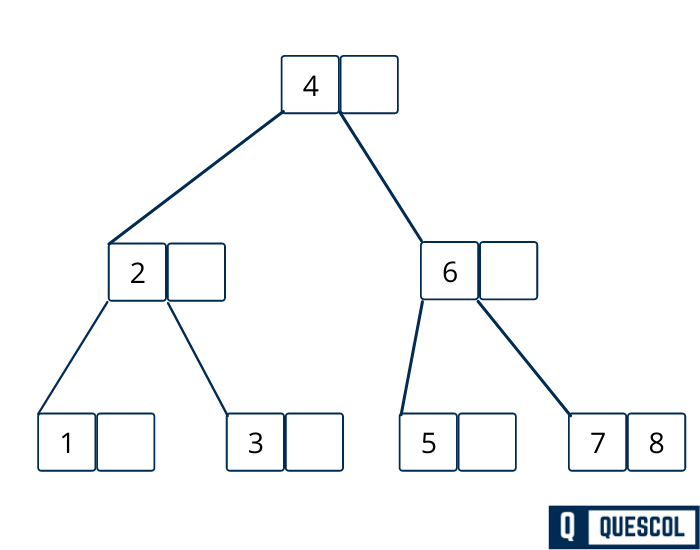
We have an B Tree of order 3 means a node can have maximum 2 keys and 3 children.
And we have to insert value 1,2,3,4,5,6,7,8 in B tree.
So Lets see how to perform insertion in B tree.
First we will insert 1 in B tree.
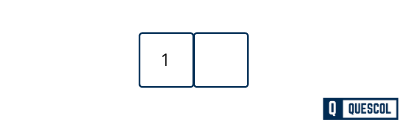
Now we will insert 2 in the B tree.
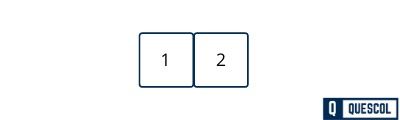
Now we have to insert 3 but as per B tree property, a node can have maximum m-1 keys where m is order of tree.
In our case a node can have maximum 2 keys. So we have to spilt the node to insert 3 in B tree.
We can insert 4 without any problem.
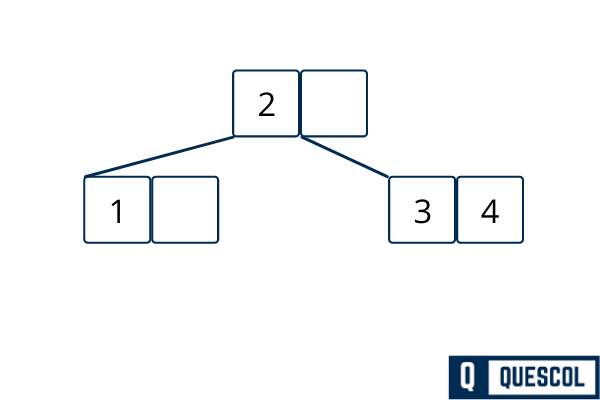
Now again we have 5 to insert but right child node is filled with 2 elements. So here we will again split it.
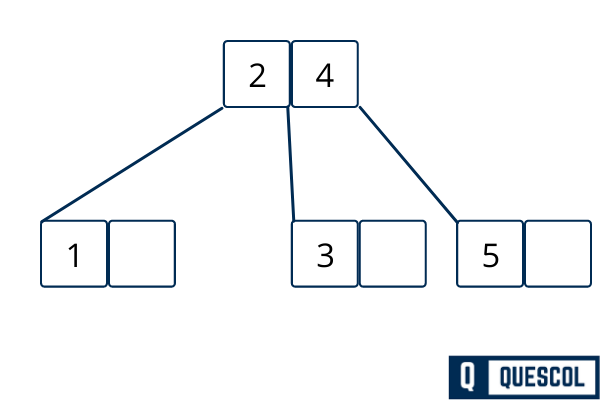
Now we can insert 6 without any problem.
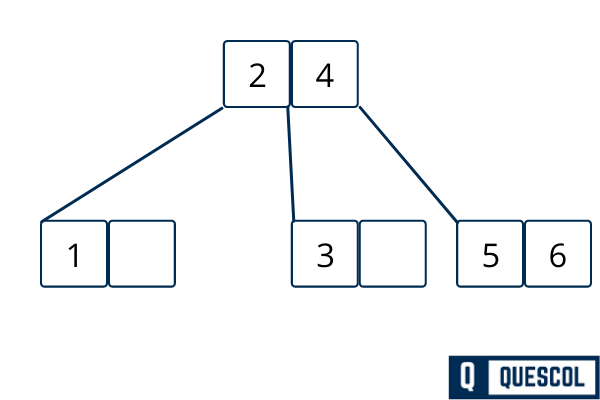
Here again we have 7 to insert but right most child node is filled with 2 elements. So here we will again split it.
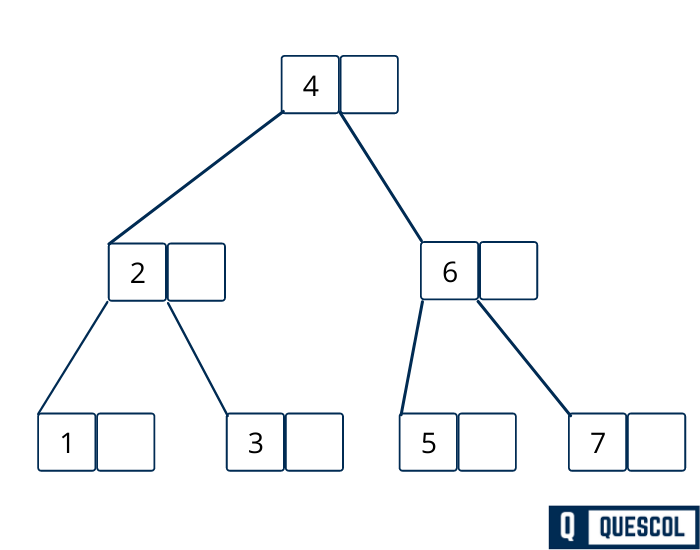
Now we can insert 8 without any problem.